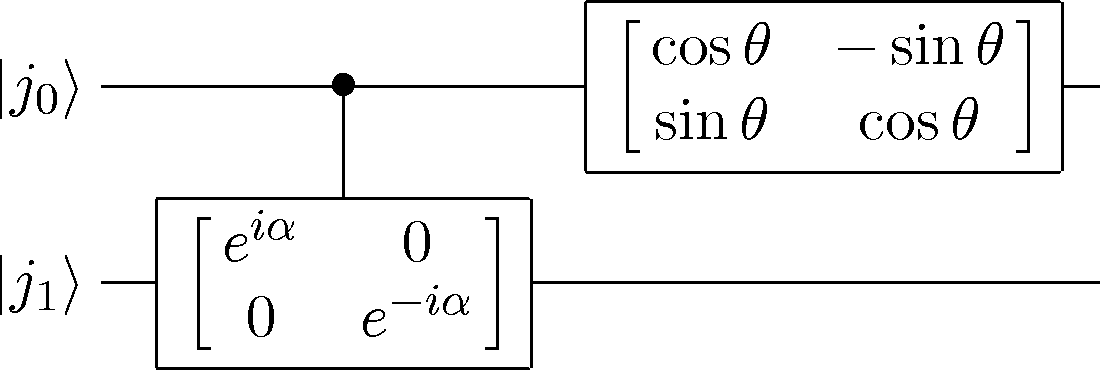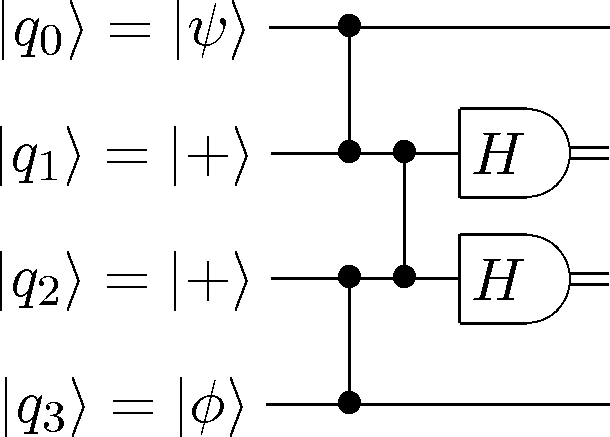Quantum Circuit Plotting with SymPy¶
Rick Muller, rpmuller@gmail.com
Explore what can and cannot be done using existing sympy circuit plotting. The initial aim will be to support everything that is on the qasm2circ website. When you see a heading listing an example number, it will refer to the example circuit on that page.
Note: The examples on this page will require at least the development (i.e. github) branch of sympy, and may require work in my current branch (which changes from week to week). If you'd like to play with newer features, and the examples on this page aren't working for you, email me (rpmuller@gmail.com) and I can send you instructions for how to get these to work.
from sympy import *
from sympy.physics.quantum.circuitplot import CircuitPlot,labeller,Mz,CreateOneQubitGate
from sympy.physics.quantum.gate import *
from sympy.physics.quantum.qasm import Qasm
Rough priorities of tasks¶
- Stack multiple gates vertically
- Block multiqubit gate
- Latex matrices as gates
- Do circuits resize correctly?
Qasm tests status¶
- Works
- Works
- Works
- Works
- Can't plot matrices as operators
- Works
- Works
- Works
- Works
- Multi-qubit blocks + classical lines
- Multi-qubit blocks
- Multi-qubit blocks
- Multi-qubit blocks (kinda works if you convert defbox->def by hand)
- Multi-qubit blocks
- D-shaped measurement
- D-shaped measurement + slash gate + vertical line gates
- D-shaped measurement
X gate test¶
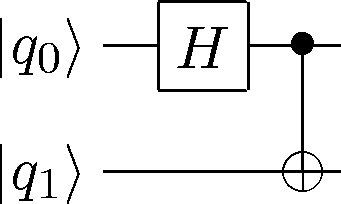
CircuitPlot(CNOT(1,0),2)
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x103844f90>
CircuitPlot(X(0),1)
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x104dec090>
Sympy now prints a normal X gate when it's a one-qubit gate, but the circ+ when it's a CNOT!
Z gate test¶
CircuitPlot(CPHASE(1,0),2)
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x104e03d10>
CircuitPlot(Z(0),1)
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x104ecba90>
Making arbitrary gates:¶
It's pretty easy to overload single-qubit operators, and you can even specify fairly complicated LaTeX:
VGate = CreateOneQubitGate('V')
SqrtX = CreateOneQubitGate('sqrt-X','\sqrt{X}')
CircuitPlot(SqrtX(0)*VGate(0),1)
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x104ee3b10>
You can even make these controlled:
CircuitPlot(CGate(1,SqrtX(0)),2)
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x104e7d690>
Unfortunately, there isn't a general way to make a block multi-qubit gate. You need to overload the plot_gate function, which I haven't. And, I guess you also have to make sure that all of the qubits are contiguous.
Todo Create multi-qubit gate.
class SqrtSWAP(TwoQubitGate):
gate_name = 'sqrt-SWAP'
gate_name_latex = u'\sqrt{SWAP}'
# This doesn't work:
# CircuitPlot(SqrtSWAP(0,1),2)
CircuitPlot(CNOT(1,0)*H(1),2,labels=labeller(2))
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x104ef0e50>
A couple of notes:
- The top wire in a figure is the nth qubit in the circuit, not the 0-th or 1st.
- The gates in a circuit are ordered left to right. In other words, the first gate to be applied is the left-most gate in the circuit.
Both of these make perfect sense from a physics point of view, but they may not be what you expect.
qasm version:¶
q = Qasm('qubit q0','qubit q1','h q0','cnot q0,q1')
q.plot()
Works, but note that I haven't implemented the subscripts in qasm parser yet. It's not hard to rewrite the labelling so that it sticks an underscore between the alphabetical characters and the numbers, but I don't want to limit the way the code works based on assumptions of use cases that I haven't fully thought through. In the meantime, if you stick underscores in the label names, these will work:
q = Qasm('qubit q_0','qubit q_1','h q_0','cnot q_0,q_1')
q.plot()
You can also call the commands directly:
q = Qasm()
q.qubit('q_0')
q.qubit('q_1')
q.h('q_0')
q.cnot('q_0','q_1')
q.plot()
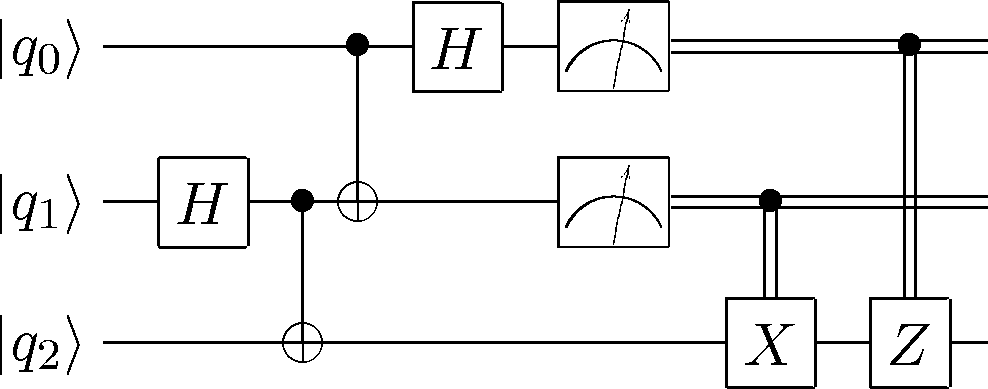
circuit = CGate(2,Z(0))*CGate(1,X(0))*Mz(2)*Mz(1)*H(2)*CNOT(2,1)*CNOT(1,0)*H(1)
cp = CircuitPlot(circuit,3,labels=labeller(3))
# qasm version
q = Qasm('qubit q_0','qubit q_1','qubit q_2','h q_1',
'cnot q_1,q_2','cnot q_0,q_1','h q_0',
'measure q_1','measure q_0',
'c-x q_1,q_2','c-z q_0,q_2')
q.plot()
CircuitPlot(CNOT(1,0)*CNOT(0,1)*CNOT(1,0),2,labels=labeller(2))
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x104fae810>
qasm version:¶
q = Qasm('qubit q_0','qubit q_1','cnot q_0,q_1','cnot q_1,q_0','cnot q_0,q_1')
q.plot()
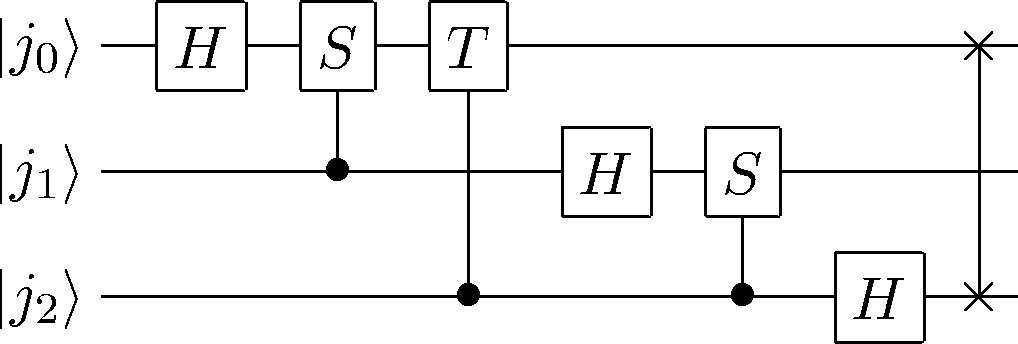
CircuitPlot(SWAP(0,2)*H(0)* CGate((0,),S(1)) *H(1)*CGate((0,),T(2))*CGate((1,),S(2))*H(2),3,labels=labeller(3,'j'))
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x104f7de50>
# qasm version:
q = Qasm("def c-S,1,'S'",
"def c-T,1,'T'",
"qubit j0",
"qubit j1",
"qubit j2",
"h j0",
"c-S j1,j0",
"c-T j2,j0",
"nop j1",
"h j1",
"c-S j2,j1",
"h j2",
"swap j0,j2")
q.plot()
# Note: you currently have to escape (double backslash) the \b and \t,
# I guess b/c they're whitespace shortcuts
class Rot1(OneQubitGate):
gate_name = 'Rot'
gate_name_latex = r'\begin{array}{ll}\cos\theta&-\sin\theta\end{array}'
# This doesn't work:
#CircuitPlot(Rot1(0),1)
U = CreateOneQubitGate('U')
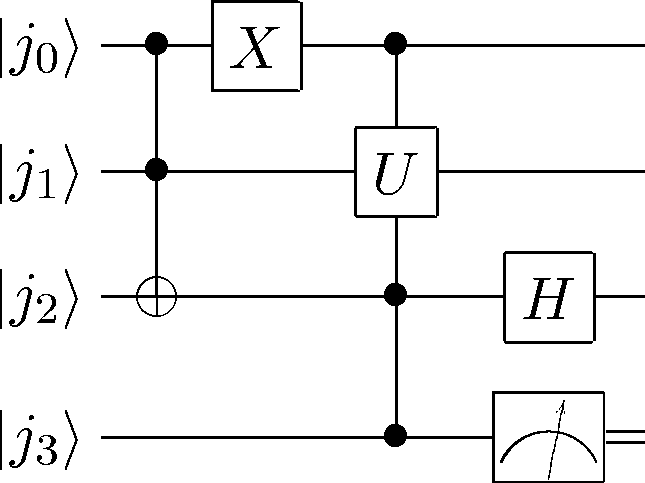
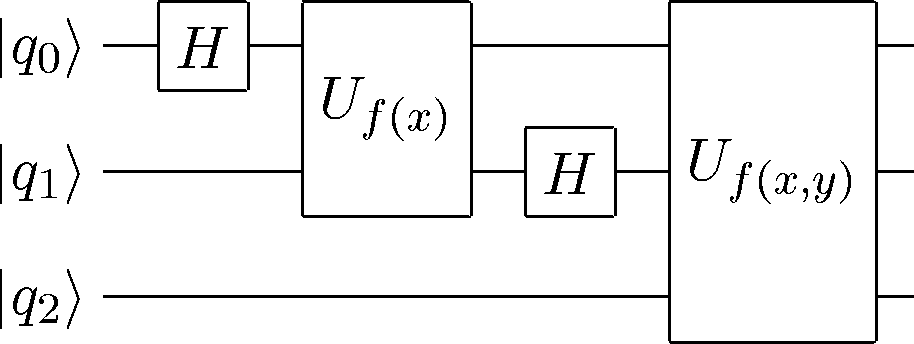
CircuitPlot(Mz(0)*H(1)*CGate((0,1,3),U(2))*X(3)*CGateS((2,3),X(1)),4,labels=labeller(4,'j'))
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x104e68c90>
# Qasm version:
q = Qasm("def c-U,3,'U'",
"qubit j0",
"qubit j1",
"qubit j2",
"qubit j3",
"toffoli j0,j1,j2",
"X j0",
"c-U j2,j3,j0,j1",
"H j2",
"measure j3")
q.plot()
V = CreateOneQubitGate('V')
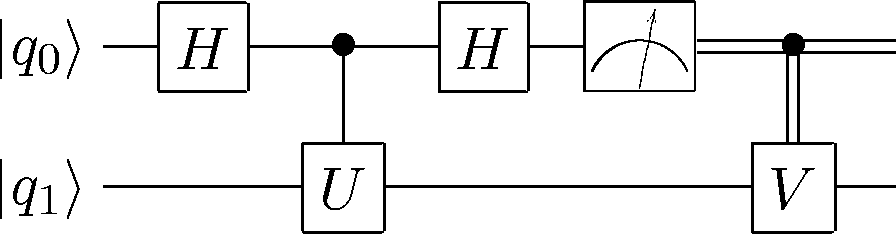
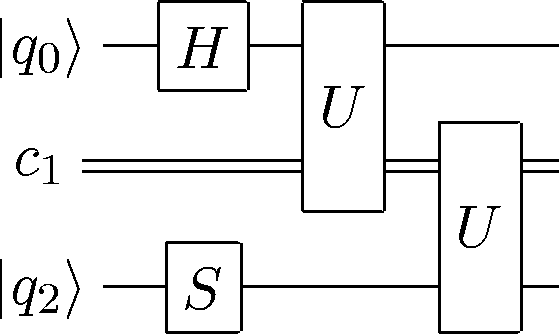
CircuitPlot(CGate(1,V(0))*Mz(1)*H(1)*CGate(1,U(0))*H(1),2,labels=labeller(2))
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x10515b450>
# Qasm
q = Qasm("def c-U,1,'U'","def c-V,1,'V'",
"qubit q0","qubit q1",
"H q0","c-U q0,q1","H q0",
"measure q0","c-V q0,q1")
q.plot()
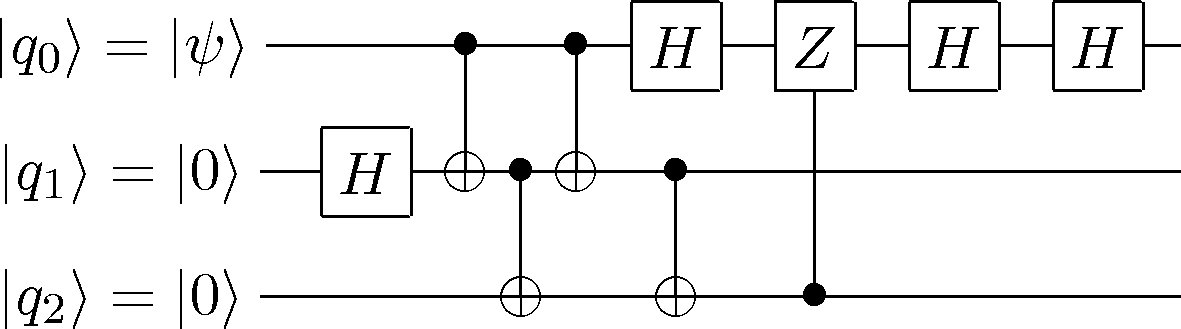
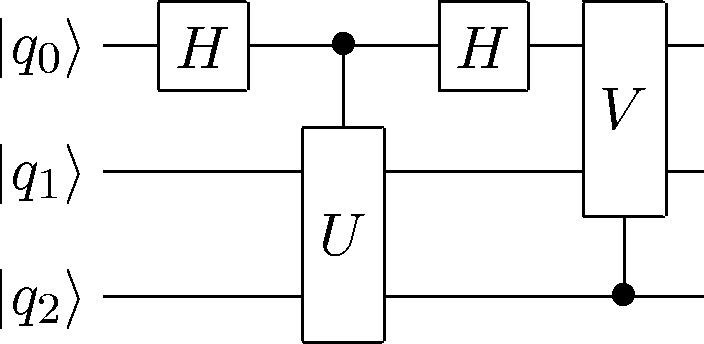
CircuitPlot(H(2)*H(2)*CGate(0,Z(2))*H(2)*CNOT(1,0)*CNOT(2,1)*CNOT(1,0)*CNOT(2,1)*H(1),3,labels=labeller(3))
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x105104c50>
#Qasm:
q = Qasm("def c-Z,1,'Z'",
"qubit q0,\psi","qubit q1,0","qubit q2,0",
"H q1","cnot q0,q1","cnot q1,q2","cnot q0,q1","cnot q1,q2",
"H q0","c-Z q2,q0","H q0","H q0")
q.plot()
SqrtX = CreateOneQubitGate('sqrt-X','\sqrt{X}')
SqrtXdag = CreateOneQubitGate('sqrt-X-dag','\sqrt{X}^\dagger')
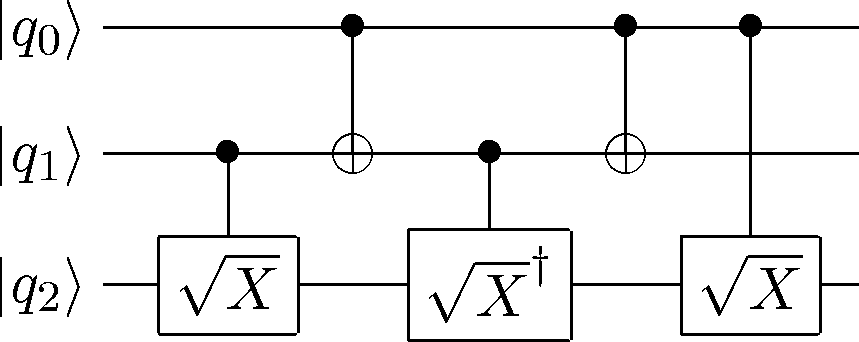
CircuitPlot(CGate(2,SqrtX(0))*CNOT(2,1)*CGate(1,SqrtXdag(0))*CNOT(2,1)*CGate(1,SqrtX(0)),3,labels=labeller(3))
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x104f62a10>
q = Qasm("def c-X,1,'\sqrt{X}'","def c-Xd,1,'{\sqrt{X}}^\dagger'",
"qubit q0","qubit q1","qubit q2",
"c-X q1,q2","cnot q0,q1","c-Xd q1,q2",
"cnot q0,q1","c-X q0,q2")
q.plot()
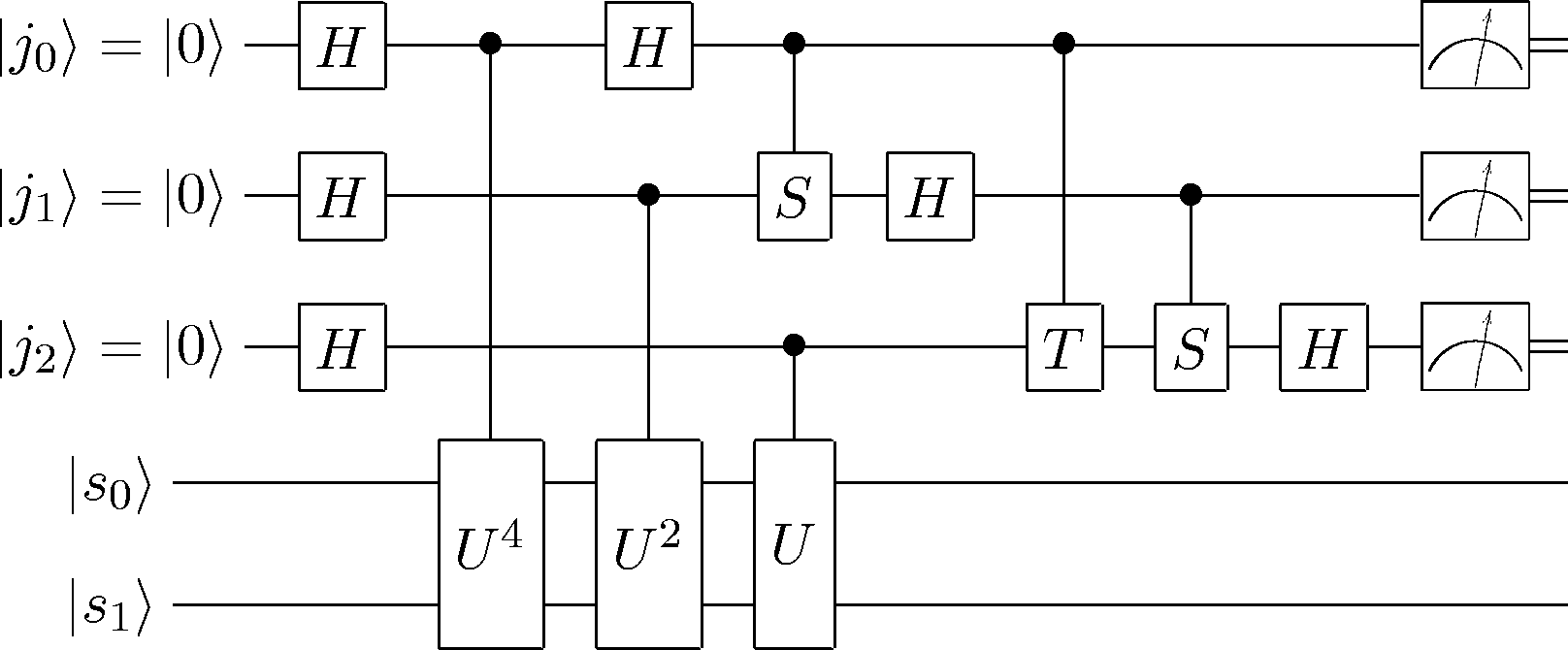
# Only works if you convert the defboxes to defs and remove qubit s2:
qasm_lines = """\
def CU,1,'U'
def CU2,1,'U^2'
def CU4,1,'U^4'
def c-S,1,'S'
def c-T,1,'T'
qubit j0,0 # QFT qubits
qubit j1,0
qubit j2,0
qubit s0 # U qubits
h j0 # equal superposition
h j1
h j2
CU4 j0,s0 # controlled-U
CU2 j1,s0
CU j2,s0
h j0 # QFT
c-S j0,j1
h j1
nop j0
c-T j0,j2
c-S j1,j2
h j2
nop j0
nop j0
nop j1
measure j0 # final measurement
measure j1
measure j2"""
q = Qasm(*qasm_lines.splitlines())
q.plot()
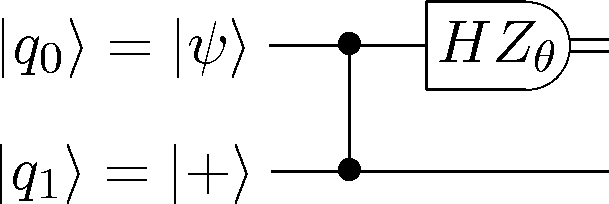
CircuitPlot(Mz(1)*CPHASE(0,1),2,labels=['+','\psi'])
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x10544ba90>
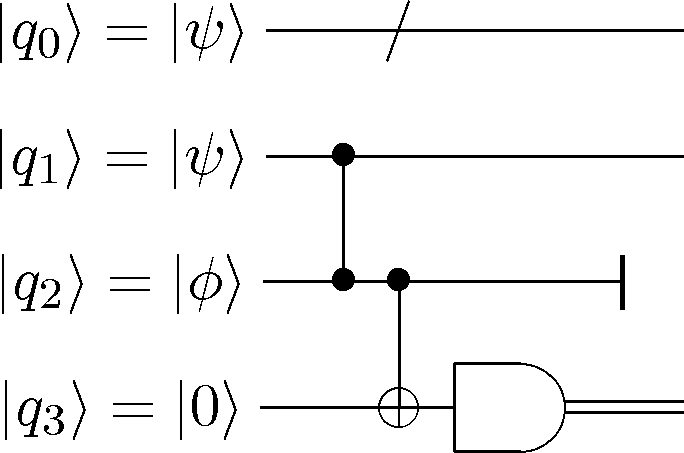
CircuitPlot(Mz(0)*CNOT(1,0)*CPHASE(1,2),4,labels=['0','\phi','\psi','\psi'])
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x105607bd0>
CircuitPlot(Mz(2)*Mz(1)*CPHASE(1,2)*CPHASE(1,0)*CPHASE(3,2),4,labels=['\phi','+','+','\psi'])
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x1050f53d0>
Surface code¶
These are the X and Z checks from a surface code:
CircuitPlot(Mz(4)*H(4)*CNOT(4,0)*CNOT(4,1)*CNOT(4,2)*CNOT(4,3)*H(4),5,labels=['d_4','d_3','d_2','d_1','a_0'])
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x105701350>
CircuitPlot(Mz(4)*CNOT(0,4)*CNOT(1,4)*CNOT(2,4)*CNOT(3,4),5,labels=['d_4','d_3','d_2','d_1','a_0'])
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x104fc2b10>
Steane code¶
Make |ˉ0⟩, Fig 12 from Aliferis, Gottesman, and Preskill.
CircuitPlot(CNOT(6,0)*CNOT(5,4)*CNOT(3,2)*CNOT(5,1)*CNOT(3,0)*CNOT(6,2)*CNOT(6,4)*CNOT(3,0),
7,labels=["0","0","0","+","0","+","+"])
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x105862d50>
Let's use the power of python to make this a little easier:
import operator
def prod(c): return reduce(operator.mul, c, 1)
steane_pairs = [(6,0),(5,4),(3,2),(5,1),(3,0),(6,2),(6,4),(3,0)]
circuit2 = prod([CNOT(i,j) for i,j in steane_pairs])
labels=["0","0","0","+","0","+","+"]
CircuitPlot(circuit2,7,labels=labels)
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x1059d0b50>
We can now extend this to a full Steane check:
circuit1 = prod([CNOT(i+7,j+7) for i,j in steane_pairs])
decoder = prod([CNOT(i+7,j+7) for i,j in reversed(steane_pairs)])
transverse = prod([CPHASE(i+7,i) for i in range(7)])
CircuitPlot(decoder*transverse*circuit2*circuit1,14,labels=labels+labels)
<sympy.physics.quantum.circuitplot.CircuitPlot at 0x1059c6b90>
That's only 7 real lines of code to plot the encoding.