Python for Data Science¶
Joe McCarthy, Data Scientist, Indeed
from IPython.display import display, Image, HTML
1. Introduction¶
 This short primer on Python is designed to provide a rapid "on-ramp" to enable computer programmers who are already familiar with concepts and constructs in other programming languages learn enough about Python to facilitate the effective use of open-source and proprietary Python-based machine learning and data science tools.
This short primer on Python is designed to provide a rapid "on-ramp" to enable computer programmers who are already familiar with concepts and constructs in other programming languages learn enough about Python to facilitate the effective use of open-source and proprietary Python-based machine learning and data science tools.
 The primer is motivated, in part, by the approach taken in the Natural Language Toolkit (NLTK) book, which provides a rapid on-ramp for using Python and the open-source NLTK library to develop programs using natural language processing techniques (many of which involve machine learning).
The primer is motivated, in part, by the approach taken in the Natural Language Toolkit (NLTK) book, which provides a rapid on-ramp for using Python and the open-source NLTK library to develop programs using natural language processing techniques (many of which involve machine learning).
The Python Tutorial offers a more comprehensive primer, and opens with an excellent - if biased - overview of some of the general strengths of the Python programming language:
Python is an easy to learn, powerful programming language. It has efficient high-level data structures and a simple but effective approach to object-oriented programming. Python’s elegant syntax and dynamic typing, together with its interpreted nature, make it an ideal language for scripting and rapid application development in many areas on most platforms.
 Hans Petter Langtangen, author of Python Scripting for Computational Science, emphasizes the utility of Python for many of the common tasks in all areas of computational science:
Hans Petter Langtangen, author of Python Scripting for Computational Science, emphasizes the utility of Python for many of the common tasks in all areas of computational science:
Very often programming is about shuffling data in and out of different tools, converting one data format to another, extracting numerical data from a text, and administering numerical experiments involving a large number of data files and directories. Such tasks are much faster to accomplish in a language like Python than in Fortran, C, C++, C#, or Java
Foster Provost, co-author of Data Science for Business, describes why Python is such a useful programming language for practical data science in Python: A Practical Tool for Data Science, :
The practice of data science involves many interrelated but different activities, including accessing data, manipulating data, computing statistics about data, plotting/graphing/visualizing data, building predictive and explanatory models from data, evaluating those models on yet more data, integrating models into production systems, etc. One option for the data scientist is to learn several different software packages that each specialize in one or two of these things, but don’t do them all well, plus learn a programming language to tie them together. (Or do a lot of manual work.)
An alternative is to use a general-purpose, high-level programming language that provides libraries to do all these things. Python is an excellent choice for this. It has a diverse range of open source libraries for just about everything the data scientist will do. It is available everywhere; high performance python interpreters exist for running your code on almost any operating system or architecture. Python and most of its libraries are both open source and free. Contrast this with common software packages that are available in a course via an academic license, yet are extremely expensive to license and use in industry.
 The goal of this primer is to provide efficient and sufficient scaffolding for software engineers with no prior knowledge of Python to be able to effectively use Python-based tools for data science research and development, such as the open-source library scikit-learn. There is another, more comprehensive tutorial for scikit-learn, Python Scientific Lecture Notes, that includes coverage of a number of other useful Python open-source libraries used by scikit-learn (numpy, scipy and matplotlib) - all highly recommended ... and, to keep things simple, all beyond the scope of this primer.
The goal of this primer is to provide efficient and sufficient scaffolding for software engineers with no prior knowledge of Python to be able to effectively use Python-based tools for data science research and development, such as the open-source library scikit-learn. There is another, more comprehensive tutorial for scikit-learn, Python Scientific Lecture Notes, that includes coverage of a number of other useful Python open-source libraries used by scikit-learn (numpy, scipy and matplotlib) - all highly recommended ... and, to keep things simple, all beyond the scope of this primer.
Using an IPython Notebook as a delivery vehicle for this primer was motivated by Brian Granger's inspiring tutorial, The IPython Notebook: Get Close to Your Data with Python and JavaScript, one of the highlights from my Strata 2014 conference experience. You can run this notebook locally in a browser once you install ipython notebook.
One final note on external resources: the Python Style Guide (PEP-0008) offers helpful tips on how best to format Python code. Code like a Pythonista offers a number of additional tips on Python programming style and philosophy, several of which are incorporated into this primer.
We will focus entirely on using Python within the interpreter environment (as supported within an IPython Notebook). Python scripts - files containing definitions of functions and variables, and typically including code invoking some of those functions - can also be run from a command line. Using Python scripts from the command line may be the subject of a future primer.
To help motivate the data science-oriented Python programming examples provided in this primer, we will start off with a brief overview of basic concepts and terminology in data science.
2. Data Science: Basic Concepts¶
Data Science and Data Mining¶
 Foster Provost and Tom Fawcett offer succinct descriptions of data science and data mining in Data Science for Business:
Foster Provost and Tom Fawcett offer succinct descriptions of data science and data mining in Data Science for Business:
Data science involves principles, processes and techniques for understanding phenomena via the (automated) analysis of data.
Data mining is the extraction of knowledge from data, via technologies that incorporate these principles.
Knowledge Discovery, Data Mining and Machine Learning¶
Provost & Fawcett also offer some history and insights into the relationship between data mining and machine learning, terms which are often used somewhat interchangeably:
The field of Data Mining (or KDD: Knowledge Discovery and Data Mining) started as an offshoot of Machine Learning, and they remain closely linked. Both fields are concerned with the analysis of data to find useful or informative patterns. Techniques and algorithms are shared between the two; indeed, the areas are so closely related that researchers commonly participate in both communities and transition between them seamlessly. Nevertheless, it is worth pointing out some of the differences to give perspective.
Speaking generally, because Machine Learning is concerned with many types of performance improvement, it includes subfields such as robotics and computer vision that are not part of KDD. It also is concerned with issues of agency and cognition — how will an intelligent agent use learned knowledge to reason and act in its environment — which are not concerns of Data Mining.
Historically, KDD spun off from Machine Learning as a research field focused on concerns raised by examining real-world applications, and a decade and a half later the KDD community remains more concerned with applications than Machine Learning is. As such, research focused on commercial applications and business issues of data analysis tends to gravitate toward the KDD community rather than to Machine Learning. KDD also tends to be more concerned with the entire process of data analytics: data preparation, model learning, evaluation, and so on.
Cross Industry Standard Process for Data Mining (CRISP-DM)¶
The Cross Industry Standard Process for Data Mining introduced a process model for data mining in 2000 that has become widely adopted.
The model emphasizes the *iterative* nature of the data mining process, distinguishing several different stages that are regularly revisited in the course of developing and deploying data-driven solutions to business problems:
- Business understanding
- Data understanding
- Data preparation
- Modeling
- Deployment
We will be focusing primarily on using Python for data preparation and modeling.
Data Science Workflow¶
Philip Guo presents a Data Science Workflow offering a slightly different process model emhasizing the importance of reflection and some of the meta-data, data management and bookkeeping challenges that typically arise in the data science process. His 2012 PhD thesis, Software Tools to Facilitate Research Programming, offers an insightful and more comprehensive description of many of these challenges.
Provost & Fawcett list a number of different tasks in which data science techniques are employed:
- Classification and class probability estimation
- Regression (aka value estimation)
- Similarity matching
- Clustering
- Co-occurrence grouping (aka frequent itemset mining, association rule discovery, market-basket analysis)
- Profiling (aka behavior description, fraud / anomaly detection)
- Link prediction
- Data reduction
- Causal modeling
We will be focusing primarily on classification and class probability estimation tasks, which are defined by Provost & Fawcett as follows:
Classification and class probability estimation attempt to predict, for each individual in a population, which of a (small) set of classes this individual belongs to. Usually the classes are mutually exclusive. An example classification question would be: “Among all the customers of MegaTelCo, which are likely to respond to a given offer?” In this example the two classes could be called will respond and will not respond.
To further simplify this primer, we will focus exclusively on supervised methods, in which the data is explicitly labeled with classes. There are also unsupervised methods that involve working with data in which there are no pre-specified class labels.
Supervised Classification¶
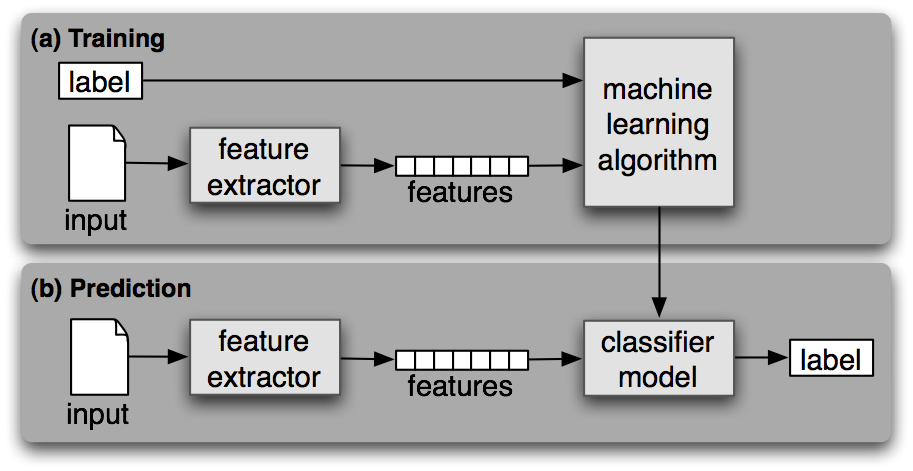
The Natural Language Toolkit (NLTK) book provides a diagram and succinct description (below, with italics and bold added for emphasis) of supervised classification:
Supervised Classification. (a) During training, a feature extractor is used to convert each input value to a feature set. These feature sets, which capture the basic information about each input that should be used to classify it, are discussed in the next section. Pairs of feature sets and labels are fed into the machine learning algorithm to generate a model. (b) During prediction, the same feature extractor is used to convert unseen inputs to feature sets. These feature sets are then fed into the model, which generates predicted labels.
Data Mining Terminology¶
- Structured data has simple, well-defined patterns (e.g., a table or graph)
- Unstructured data has less well-defined patterns (e.g., text, images)
- Model: a pattern that captures / generalizes regularities in data (e.g., an equation, set of rules, decision tree)
- Attribute (aka variable, feature, signal, column): an element used in a model
- Instance (aka example, feature vector, row): a representation of a single entity being modeled
- Target attribute (aka dependent variable, class label): the class / type / category of an entity being modeled
Data Mining Example: UCI Mushroom dataset¶
The Center for Machine Learning and Intelligent Systems at the University of California, Irvine (UCI), hosts a Machine Learning Repository containing over 200 publicly available data sets.
 We will use the mushroom data set, which forms the basis of several examples in Chapter 3 of the Provost & Fawcett data science book.
We will use the mushroom data set, which forms the basis of several examples in Chapter 3 of the Provost & Fawcett data science book.
The following description of the dataset is provided at the UCI repository:
This data set includes descriptions of hypothetical samples corresponding to 23 species of gilled mushrooms in the Agaricus and Lepiota Family (pp. 500-525 [The Audubon Society Field Guide to North American Mushrooms, 1981]). Each species is identified as definitely edible, definitely poisonous, or of unknown edibility and not recommended. This latter class was combined with the poisonous one. The Guide clearly states that there is no simple rule for determining the edibility of a mushroom; no rule like leaflets three, let it be'' for Poisonous Oak and Ivy.
Number of Instances: 8124
Number of Attributes: 22 (all nominally valued)
Attribute Information: (classes: edible=e, poisonous=p)
- cap-shape: bell=b, conical=c, convex=x, flat=f, knobbed=k, sunken=s
- cap-surface: fibrous=f, grooves=g, scaly=y, smooth=s
- cap-color: brown=n ,buff=b, cinnamon=c, gray=g, green=r, pink=p, purple=u, red=e, white=w, yellow=y
- bruises?: bruises=t, no=f
- odor: almond=a, anise=l, creosote=c, fishy=y, foul=f, musty=m, none=n, pungent=p, spicy=s
- gill-attachment: attached=a, descending=d, free=f, notched=n
- gill-spacing: close=c, crowded=w, distant=d
- gill-size: broad=b, narrow=n
- gill-color: black=k, brown=n, buff=b, chocolate=h, gray=g, green=r, orange=o, pink=p, purple=u, red=e, white=w, yellow=y
- stalk-shape: enlarging=e, tapering=t
- stalk-root: bulbous=b, club=c, cup=u, equal=e, rhizomorphs=z, rooted=r, missing=?
- stalk-surface-above-ring: fibrous=f, scaly=y, silky=k, smooth=s
- stalk-surface-below-ring: fibrous=f, scaly=y, silky=k, smooth=s
- stalk-color-above-ring: brown=n, buff=b, cinnamon=c, gray=g, orange=o, pink=p, red=e, white=w, yellow=y
- stalk-color-below-ring: brown=n, buff=b, cinnamon=c, gray=g, orange=o, pink=p, red=e, white=w, yellow=y
- veil-type: partial=p, universal=u
- veil-color: brown=n, orange=o, white=w, yellow=y
- ring-number: none=n, one=o, two=t
- ring-type: cobwebby=c, evanescent=e, flaring=f, large=l, none=n, pendant=p, sheathing=s, zone=z
- spore-print-color: black=k, brown=n, buff=b, chocolate=h, green=r, orange=o, purple=u, white=w, yellow=y
- population: abundant=a, clustered=c, numerous=n, scattered=s, several=v, solitary=y
- habitat: grasses=g, leaves=l, meadows=m, paths=p, urban=u, waste=w, woods=d
Missing Attribute Values: 2480 of them (denoted by "?"), all for attribute #11.
Class Distribution: -- edible: 4208 (51.8%) -- poisonous: 3916 (48.2%) -- total: 8124 instances
The data file associated with this dataset has one instance of a hypothetical mushroom per line, with abbreviations for the values of the class and each of the other 22 attributes separated by commas.
Here is a sample line from the data file:
p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d
This instance represents a mushroom with the following attribute values (highlighted in bold):
class: edible=e, poisonous=p
- cap-shape: bell=b, conical=c, convex=x, flat=f, knobbed=k, sunken=s
- cap-surface: fibrous=f, grooves=g, scaly=y, smooth=s
- cap-color: brown=n ,buff=b, cinnamon=c, gray=g, green=r, pink=p, purple=u, red=e, white=w, yellow=y
- bruises?: bruises=t, no=f
- odor: almond=a, anise=l, creosote=c, fishy=y, foul=f, musty=m, none=n, pungent=p, spicy=s
- gill-attachment: attached=a, descending=d, free=f, notched=n
- gill-spacing: close=c, crowded=w, distant=d
- gill-size: broad=b, narrow=n
- gill-color: black=k, brown=n, buff=b, chocolate=h, gray=g, green=r, orange=o, pink=p, purple=u, red=e, white=w, yellow=y
- stalk-shape: enlarging=e, tapering=t
- stalk-root: bulbous=b, club=c, cup=u, equal=e, rhizomorphs=z, rooted=r, missing=?
- stalk-surface-above-ring: fibrous=f, scaly=y, silky=k, smooth=s
- stalk-surface-below-ring: fibrous=f, scaly=y, silky=k, smooth=s
- stalk-color-above-ring: brown=n, buff=b, cinnamon=c, gray=g, orange=o, pink=p, red=e, white=w, yellow=y
- stalk-color-below-ring: brown=n, buff=b, cinnamon=c, gray=g, orange=o, pink=p, red=e, white=w, yellow=y
- veil-type: partial=p, universal=u
- veil-color: brown=n, orange=o, white=w, yellow=y
- ring-number: none=n, one=o, two=t
- ring-type: cobwebby=c, evanescent=e, flaring=f, large=l, none=n, pendant=p, sheathing=s, zone=z
- spore-print-color: black=k, brown=n, buff=b, chocolate=h, green=r, orange=o, purple=u, white=w, yellow=y
- population: abundant=a, clustered=c, numerous=n, scattered=s, several=v, solitary=y
- habitat: grasses=g, leaves=l, meadows=m, paths=p, urban=u, waste=w, woods=d
Building a model with this data set will serve as a motivating example throughout much of this primer.
3. Python: Basic Concepts¶
A note on Python 2 vs. Python 3¶
There are 2 major versions of Python in widespread use: Python 2 and Python 3. Python 3 has some features that are not backward compatible with Python 2, and some Python 2 libraries have not been updated to work with Python 3. I have been using Python 2, primarily because I use some of those Python 2[-only] libraries, but an increasing proportion of them are migrating to Python 3, and I anticipate shifting to Python 3 in the near future.
For more on the topic, I recommend a very well documented IPython Notebook, which includes numerous helpful examples and links, by Sebastian Raschka, Key differences between Python 2.7.x and Python 3.x, the Cheat Sheet: Writing Python 2-3 compatible code by Ed Schofield ... or googling Python 2 vs 3.
Nick Coghlan, a CPython core developer, sent me an email suggesting that relatively minor changes in this notebook would enable it to run with Python 2 or Python 3: importing the print_function from the __future__ module, and changing my print statements (Python 2) to print function calls (Python 3). Although a relatively minor conceptual change, it necessitated the changing of many individual cells to reflect the Python 3 print syntax.
I decided to import the division module from the future, as I find the use of / for "true division" - and the use of // for "floor division" - to be more aligned with my intuition. I also needed to replace a few functions that are no longer available in Python 3 with related functions that are available in both versions; I've added notes in nearby cells where the incompatible functions were removed explaining why they are related ... and no longer available.
The differences are briefly illustrated below, with print statements or function calls before and after the importing of the Python 3 versions of the print function and division operator.
print 1, "/", 2, "=", 1 / 2
1 / 2 = 0
print(1, "/", 2, "=", 1 / 2)
(1, '/', 2, '=', 0)
from __future__ import print_function, division
print 1, "/", 2, "=", 1 / 2
File "<ipython-input-5-168a26d8ec56>", line 1 print 1, "/", 2, "=", 1 / 2 ^ SyntaxError: invalid syntax
print(1, "/", 2, "=", 1 / 2)
1 / 2 = 0.5
Names (identifiers), strings & binding values to names (assignment)¶
The sample instance of a mushroom shown above can be represented as a string.
A Python *string* (str) is a sequence of 0 or more characters enclosed within a pair of single quotes (') or a pair of double quotes (").
'p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d'
'p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d'
Python identifiers (or names) are composed of letters, numbers and/or underscores ('_'), starting with a letter or underscore. Python identifiers are case sensitive. Although camelCase identifiers can be used, it is generally considered more pythonic to use underscores. Python variables and functions typically start with lowercase letters; Python classes start with uppercase letters.
The following assignment statement binds the value of the string shown above to the name single_instance_str. Typing the name on the subsequent line will cause the intepreter to print the value bound to that name.
single_instance_str = 'p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d'
single_instance_str
'p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d'
Printing¶
The print function writes the value of its comma-delimited arguments to sys.stdout (typically the console). Each value in the output is separated by a single blank space.
print('A', 'B', 'C', 1, 2, 3)
print('Instance 1:', single_instance_str)
A B C 1 2 3 Instance 1: p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d
The print function has an optional keyword argument, end. When this argument is used and its value does not include '\n' (newline character), the output cursor will not advance to the next line.
print('A', 'B') # no end argument
print('C')
print ('A', 'B', end='...\n') # end includes '\n' --> output cursor advancees to next line
print ('C')
print('A', 'B', end=' ') # end=' ' --> use a space rather than newline at the end of the line
print('C') # so that subsequent printed output will appear on same line
A B C A B... C A B C
Comments¶
The Python *comment* character is '#': anything after '#' on the line is ignored by the Python interpreter. PEP8 style guidelines recommend using at least 2 blank spaces before an inline comment that appears on the same line as any code.
*Multi-line strings* can be used within code blocks to provide multi-line comments.
Multi-line strings are delimited by pairs of triple quotes (''' or """). Any newlines in the string will be represented as '\n' characters in the string.
'''
This is
a mult-line
string'''
'\nThis is\na mult-line\nstring'
print('Before comment') # this is an inline comment
'''
This is
a multi-line
comment
'''
print('After comment')
Before comment After comment
Multi-line strings can be printed, in which case the embedded newline ('\n') characters will be converted to newlines in the output.
print('''
This is
a mult-line
string''')
This is a mult-line string
Lists¶
A list is an ordered *sequence* of 0 or more comma-delimited elements enclosed within square brackets ('[', ']'). The Python str.split(sep) method can be used to split a sep-delimited string into a corresponding list of elements.
In the following example, a comma-delimited string is split using sep=','.
single_instance_list = single_instance_str.split(',')
print(single_instance_list)
['p', 'k', 'f', 'n', 'f', 'n', 'f', 'c', 'n', 'w', 'e', '?', 'k', 'y', 'w', 'n', 'p', 'w', 'o', 'e', 'w', 'v', 'd']
Python lists are heterogeneous, i.e., they can contain elements of different types.
mixed_list = ['a', 1, 2.3, True, [1, 'b']]
print(mixed_list)
['a', 1, 2.3, True, [1, 'b']]
The Python + operator can be used for addition, and also to concatenate strings and lists.
print(1 + 2 + 3)
print('a' + 'b' + 'c')
print(['a', 1] + [2.3, True] + [[1, 'b']])
6 abc ['a', 1, 2.3, True, [1, 'b']]
Accessing sequence elements & subsequences¶
Individual elements of sequences (e.g., lists and strings) can be accessed by specifying their zero-based index position within square brackets ('[', ']').
The following statements print out the 3rd element - at zero-based index position 2 - of single_instance_str and single_instance_list.
Note that the 3rd elements are not the same, as commas count as elements in the string, but not in the list created by splitting a comma-delimited string.
print(single_instance_str)
print(single_instance_str[2])
print(single_instance_list)
print(single_instance_list[2])
p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d k ['p', 'k', 'f', 'n', 'f', 'n', 'f', 'c', 'n', 'w', 'e', '?', 'k', 'y', 'w', 'n', 'p', 'w', 'o', 'e', 'w', 'v', 'd'] f
Negative index values can be used to specify a position offset from the end of the sequence.
It is often useful to use a -1 index value to access the last element of a sequence.
print(single_instance_str)
print(single_instance_str[-1])
print(single_instance_str[-2])
p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d d ,
print(single_instance_list)
print(single_instance_list[-1])
print(single_instance_list[-2])
['p', 'k', 'f', 'n', 'f', 'n', 'f', 'c', 'n', 'w', 'e', '?', 'k', 'y', 'w', 'n', 'p', 'w', 'o', 'e', 'w', 'v', 'd'] d v
The Python *slice notation* can be used to access subsequences by specifying two index positions separated by a colon (':'); seq[start:stop] returns all the elements in seq between start and stop - 1 (inclusive).
print(single_instance_str[2:4])
print(single_instance_list[2:4])
k, ['f', 'n']
Slices index values can be negative.
print(single_instance_str[-4:-2])
print(single_instance_list[-4:-2])
,v ['e', 'w']
The start and/or stop index can be omitted. A common use of slices with a single index value is to access all but the first element or all but the last element of a sequence.
print(single_instance_str)
print(single_instance_str[:-1]) # all but the last
print(single_instance_str[:-2]) # all but the last 2
print(single_instance_str[1:]) # all but the first
print(single_instance_str[2:]) # all but the first 2
p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v, p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v ,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d
print(single_instance_list)
print(single_instance_list[:-1])
print(single_instance_list[1:])
['p', 'k', 'f', 'n', 'f', 'n', 'f', 'c', 'n', 'w', 'e', '?', 'k', 'y', 'w', 'n', 'p', 'w', 'o', 'e', 'w', 'v', 'd'] ['p', 'k', 'f', 'n', 'f', 'n', 'f', 'c', 'n', 'w', 'e', '?', 'k', 'y', 'w', 'n', 'p', 'w', 'o', 'e', 'w', 'v'] ['k', 'f', 'n', 'f', 'n', 'f', 'c', 'n', 'w', 'e', '?', 'k', 'y', 'w', 'n', 'p', 'w', 'o', 'e', 'w', 'v', 'd']
Slice notation includes an optional third element, step, as in seq[start:stop:step], that specifies the steps or increments by which elements are retrieved from seq between start and step - 1:
print(single_instance_str)
print(single_instance_str[::2]) # print elements in even-numbered positions
print(single_instance_str[1::2]) # print elements in odd-numbered positions
print(single_instance_str[::-1]) # print elements in reverse order
p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d pkfnfnfcnwe?kywnpwoewvd ,,,,,,,,,,,,,,,,,,,,,, d,v,w,e,o,w,p,n,w,y,k,?,e,w,n,c,f,n,f,n,f,k,p
The Python tutorial offers a helpful ASCII art representation to show how positive and negative indexes are interpreted:
+---+---+---+---+---+ | H | e | l | p | A | +---+---+---+---+---+ 0 1 2 3 4 5 -5 -4 -3 -2 -1
Splitting / separating statements¶
Python statements are typically separated by newlines (rather than, say, the semi-colon in Java). Statements can extend over more than one line; it is generally best to break the lines after commas, parentheses, braces or brackets. Inserting a backslash character ('\') at the end of a line will also enable continuation of the statement on the next line, but it is generally best to look for other alternatives.
attribute_names = ['class',
'cap-shape', 'cap-surface', 'cap-color',
'bruises?',
'odor',
'gill-attachment', 'gill-spacing', 'gill-size', 'gill-color',
'stalk-shape', 'stalk-root',
'stalk-surface-above-ring', 'stalk-surface-below-ring',
'stalk-color-above-ring', 'stalk-color-below-ring',
'veil-type', 'veil-color',
'ring-number', 'ring-type',
'spore-print-color',
'population',
'habitat']
print(attribute_names)
['class', 'cap-shape', 'cap-surface', 'cap-color', 'bruises?', 'odor', 'gill-attachment', 'gill-spacing', 'gill-size', 'gill-color', 'stalk-shape', 'stalk-root', 'stalk-surface-above-ring', 'stalk-surface-below-ring', 'stalk-color-above-ring', 'stalk-color-below-ring', 'veil-type', 'veil-color', 'ring-number', 'ring-type', 'spore-print-color', 'population', 'habitat']
print('a', 'b', 'c', # no '\' needed when breaking after comma
1, 2, 3)
a b c 1 2 3
print( # no '\' needed when breaking after parenthesis, brace or bracket
'a', 'b', 'c',
1, 2, 3)
a b c 1 2 3
print(1 + 2 \
+ 3)
6
Processing strings & other sequences¶
The str.strip([chars]) method returns a copy of str in which any leading or trailing chars are removed. If no chars are specified, it removes all leading and trailing whitespace. [Whitespace is any sequence of spaces, tabs ('\t') and/or newline ('\n') characters.]
Note that since a blank space is inserted in the output after every item in a comma-delimited list, the second asterisk below is printed after a leading blank space is inserted on the new line.
print('*', '\tp,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d\n', '*')
* p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d *
print('*', '\tp,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d\n'.strip(), '*')
* p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d *
print('*', '\tp,k,f,n,f,n,f,c,n,w,e, ?,k,y\t,w,n,p,w\n,o,e,w,v,d\n'.strip(), '*')
* p,k,f,n,f,n,f,c,n,w,e, ?,k,y ,w,n,p,w ,o,e,w,v,d *
A common programming pattern when dealing with CSV (comma-separated value) files, such as the mushroom dataset file mentioned above, is to repeatedly:
- read a line from a file
- strip off any leading and trailing whitespace
- split the values separated by commas into a list
We will get to repetition control structures (loops) and file input and output shortly, but here is an example of how str.strip() and str.split() be chained together in a single instruction for processing a line representing a single instance from the mushroom dataset file. Note that chained methods are executed in left-to-right order.
[Python providees a csv* module to facilitate the processing of CSV files, but we will not use that module here]*
single_instance_str = 'p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d\n'
print(single_instance_str)
# first strip leading & trailing whitespace, then split on commas
single_instance_list = single_instance_str.strip().split(',')
print(single_instance_list)
p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d ['p', 'k', 'f', 'n', 'f', 'n', 'f', 'c', 'n', 'w', 'e', '?', 'k', 'y', 'w', 'n', 'p', 'w', 'o', 'e', 'w', 'v', 'd']
The str.join(words) method is the inverse of str.split(), returning a single string in which each string in the sequence of words is separated by str.
print(single_instance_list)
print(','.join(single_instance_list))
['p', 'k', 'f', 'n', 'f', 'n', 'f', 'c', 'n', 'w', 'e', '?', 'k', 'y', 'w', 'n', 'p', 'w', 'o', 'e', 'w', 'v', 'd'] p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d
A number of Python methods can be used on strings, lists and other sequences.
The len(s) function can be used to find the length of (number of items in) a sequence s. It will also return the number of items in a dictionary, a data structure we will cover further below.
print(len(single_instance_str))
print(len(single_instance_list))
46 23
The in operator can be used to determine whether a sequence contains a value.
Boolean values in Python are True and False (note the capitalization).
print(',' in single_instance_str)
print(',' in single_instance_list)
True False
The s.count(x) ormethod can be used to count the number of occurrences of item x in sequence s.
print(single_instance_str.count(','))
print(single_instance_list.count('f'))
22 3
The s.index(x) method can be used to find the first zero-based index of item x in sequence s.
print(single_instance_str.index(','))
print(single_instance_list.index('f'))
1 2
Note that an ValueError exception will be raised if item x is not found in sequence s.
print(single_instance_list.index(','))
--------------------------------------------------------------------------- ValueError Traceback (most recent call last) <ipython-input-38-062ca5cc211d> in <module>() ----> 1 print(single_instance_list.index(',')) ValueError: ',' is not in list
Mutability¶
One important distinction between strings and lists has to do with their mutability.
Python strings are immutable, i.e., they cannot be modified. Most string methods (like str.strip()) return modified copies of the strings on which they are used.
Python lists are mutable, i.e., they can be modified.
The examples below illustrate a number of list methods that modify lists.
list_1 = [1, 2, 3, 5, 1]
list_2 = list_1 # list_2 now references the same object as list_1
print('list_1: ', list_1)
print('list_2: ', list_2)
print()
list_1.remove(1) # remove [only] the first occurrence of 1 in list_1
print('list_1.remove(1): ', list_1)
print()
list_1.pop(2) # remove the element in position 2
print('list_1.pop(2): ', list_1)
print()
list_1.append(6) # add 6 to the end of list_1
print('list_1.append(6): ', list_1)
print()
list_1.insert(0, 7) # add 7 to the beinning of list_1 (before the element in position 0)
print('list_1.insert(0, 7):', list_1)
print()
list_1.sort()
print('list_1.sort(): ', list_1)
print()
list_1.reverse()
print('list_1.reverse(): ', list_1)
list_1: [1, 2, 3, 5, 1] list_2: [1, 2, 3, 5, 1] list_1.remove(1): [2, 3, 5, 1] list_1.pop(2): [2, 3, 1] list_1.append(6): [2, 3, 1, 6] list_1.insert(0, 7): [7, 2, 3, 1, 6] list_1.sort(): [1, 2, 3, 6, 7] list_1.reverse(): [7, 6, 3, 2, 1]
When more than one name (e.g., a variable) is bound to the same mutable object, changes made to that object are reflected in all names bound to that object. For example, in the second statement above, list_2 is bound to the same object that is bound to list_1. All changes made to the object bound to list_1 will thus be reflected in list_2 (since they both reference the same object).
print('list_1: ', list_1)
print('list_2: ', list_2)
list_1: [7, 6, 3, 2, 1] list_2: [7, 6, 3, 2, 1]
We can create a copy of a list by using slice notation and not specifying a start or end parameter, i.e., [:], and if we assign that copy to another variable, the variables will be bound to different objects, so changes to one do not affect the other.
list_1 = [1, 2, 3, 5, 1]
list_2 = list_1[:] # list_1[:] returns a copy of the entire contents of list_1
print('list_1: ', list_1)
print('list_2: ', list_2)
print()
list_1.remove(1) # remove [only] the first occurrence of 1 in list_1
print('list_1.remove(1): ', list_1)
print()
print('list_1: ', list_1)
print('list_2: ', list_2)
list_1: [1, 2, 3, 5, 1] list_2: [1, 2, 3, 5, 1] list_1.remove(1): [2, 3, 5, 1] list_1: [2, 3, 5, 1] list_2: [1, 2, 3, 5, 1]
The dir() function returns all the attributes associated with a Python name (e.g., a variable) in alphabetical order.
When invoked with a name bound to a list object, it will return the methods that can be invoked on a list. The attributes with leading and trailing underscores should be treated as protected (i.e., they should not be used); we'll discuss this further below.
dir(list_1)
['__add__', '__class__', '__contains__', '__delattr__', '__delitem__', '__delslice__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__getitem__', '__getslice__', '__gt__', '__hash__', '__iadd__', '__imul__', '__init__', '__iter__', '__le__', '__len__', '__lt__', '__mul__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__reversed__', '__rmul__', '__setattr__', '__setitem__', '__setslice__', '__sizeof__', '__str__', '__subclasshook__', 'append', 'count', 'extend', 'index', 'insert', 'pop', 'remove', 'reverse', 'sort']
There are sorting and reversing functions, sorted() and reversed(), that do not modify their arguments, and can thus be used on mutable or immutable objects.
Note that sorted() always returns a sorted list of each element in its argument, regardless of which type of sequence it is passed. Thus, invoking sorted() on a string returns a list of sorted characters from the string, rather than a sorted string.
print('sorted(list_1):', sorted(list_1))
print('list_1: ', list_1)
print()
print('sorted(single_instance_str):', sorted(single_instance_str))
print('single_instance_str: ', single_instance_str)
sorted(list_1): [1, 2, 3, 5] list_1: [2, 3, 5, 1] sorted(single_instance_str): ['\n', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', '?', 'c', 'd', 'e', 'e', 'f', 'f', 'f', 'k', 'k', 'n', 'n', 'n', 'n', 'o', 'p', 'p', 'v', 'w', 'w', 'w', 'w', 'y'] single_instance_str: p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d
The sorted() function sorts its argument in ascending order by default.
An optional *keyword argument*, reverse, can be used to sort in descending order. The default value of this optional parameter is False; to get non-default behavior of an optional argument, we must specify the name and value of the argument, in this case, reverse=True.
print(sorted(single_instance_str))
print(sorted(single_instance_str, reverse=True))
['\n', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', '?', 'c', 'd', 'e', 'e', 'f', 'f', 'f', 'k', 'k', 'n', 'n', 'n', 'n', 'o', 'p', 'p', 'v', 'w', 'w', 'w', 'w', 'y'] ['y', 'w', 'w', 'w', 'w', 'v', 'p', 'p', 'o', 'n', 'n', 'n', 'n', 'k', 'k', 'f', 'f', 'f', 'e', 'e', 'd', 'c', '?', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', ',', '\n']
Tuples (immutable list-like sequences)¶
A tuple is an ordered, immutable sequence of 0 or more comma-delimited values enclosed in parentheses ('(', ')'). Many of the functions and methods that operate on strings and lists also operate on tuples.
x = (5, 4, 3, 2, 1) # a tuple
print('x =', x)
print('len(x) =', len(x))
print('x.index(3) =', x.index(3))
print('x[2:4] = ', x[2:4])
print('x[4:2:-1] = ', x[4:2:-1])
print('sorted(x):', sorted(x)) # note: sorted() always returns a list
x = (5, 4, 3, 2, 1) len(x) = 5 x.index(3) = 2 x[2:4] = (3, 2) x[4:2:-1] = (1, 2) sorted(x): [1, 2, 3, 4, 5]
Note that the methods that modify lists (e.g., append(), remove(), reverse(), sort()) are not defined for immutable sequences such as tuples (or strings). Invoking one of these sequence modification methods on an immutable sequence will raise an AttributeError exception.
x.append(6)
--------------------------------------------------------------------------- AttributeError Traceback (most recent call last) <ipython-input-46-12939164f245> in <module>() ----> 1 x.append(6) AttributeError: 'tuple' object has no attribute 'append'
However, one can approximate these modifications by creating modified copies of an immutable sequence and then re-assigning it to a name.
x = x + (6,) # need to include a comma to differentiate tuple from numeric expression
x
(5, 4, 3, 2, 1, 6)
Note that Python has a += operator which is a shortcut for the name = name + new_value pattern. This can be used for addition (e.g., x += 1 is shorthand for x = x + 1) or concatenation (e.g., x += (7,) is shorthand for x = x + (7,)).
x += (7,)
x
(5, 4, 3, 2, 1, 6, 7)
A tuple of one element must include a trailing comma to differentiate it from a parenthesized expression.
('a')
'a'
('a',)
('a',)
Conditionals¶
One common approach to handling errors is to look before you leap (LBYL), i.e., test for potential exceptions before executing instructions that might raise those exceptions.
This approach can be implemented using the if statement (which may optionally include an else and any number of elif clauses).
The following is a simple example of an if statement:
class_value = 'x' # try changing this to 'p' or 'x'
if class_value == 'e':
print('edible')
elif class_value == 'p':
print('poisonous')
else:
print('unknown')
unknown
Note that
- a colon ('
:') is used at the end of the lines withif,elseorelif - no parentheses are required to enclose the boolean condition (it is presumed to include everything between
iforelifand the colon) - the statements below each
if,elifandelseline are all indented
Python does not have special characters to delimit statement blocks (like the '{' and '}' delimiters in Java); instead, sequences of statements with the same indentation level are treated as a statement block. The Python Style Guide recommends using 4 spaces for each indentation level.
An if statement can be used to follow the LBYL paradigm in preventing the ValueError that occured in an earlier example:
attribute = 'bruises?' # try substituting 'bruises?' for 'bruises' and re-running this code
if attribute in attribute_names:
i = attribute_names.index(attribute)
print(attribute, 'is in position', i)
else:
print(attribute, 'is not in', attribute_names)
bruises? is in position 4
Seeking forgiveness vs. asking for permission (EAFP vs. LBYL)¶
Another perspective on handling errors championed by some pythonistas is that it is easier to ask forgiveness than permission (EAFP).
As in many practical applications of philosophy, religion or dogma, it is helpful to think before you choose (TBYC). There are a number of factors to consider in deciding whether to follow the EAFP or LBYL paradigm, including code readability and the anticipated likelihood and relative severity of encountering an exception. For those who are interested, Oran Looney wrote a blog post providing a nice overview of the debate over LBYL vs. EAFP.
In keeping with practices most commonly used with other languages, we will follow the LBYL paradigm throughout most of this primer.
However, as a brief illustration of the EAFP paradigm in Python, here is an alternate implementation of the functionality of the code above, using a try/except statement.
attribute = 'bruises?' # try substituting 'bruises' for 'bruises' and re-running this code
i = -1
try:
i = attribute_names.index(attribute)
print(attribute, 'is in position', i)
except ValueError:
print(attribute, 'is not found')
bruises? is in position 4
There is no local scoping inside a try, so the value of i persists after the try/except statement.
i
4
The Python null object is None (note the capitalization).
attribute = 'bruises' # try substituting 'bruises?' for 'bruises' and re-running this code
if attribute not in attribute_names: # equivalent to 'not attribute in attribute_names'
value = None
else:
i = attribute_names.index(attribute)
value = single_instance_list[i]
print(attribute, '=', value)
bruises = None
Defining and calling functions¶
Python function definitions start with the def keyword followed by a function name, a list of 0 or more comma-delimited parameters (aka 'formal parameters') enclosed within parentheses, and then a colon (':').
A function definition may include one or more return statements to indicate the value(s) returned to where the function is called. It is good practice to include a short docstring to briefly describe the behavior of the function and the value(s) it returns.
def attribute_value(instance, attribute, attribute_names):
'''Returns the value of attribute in instance, based on its position in attribute_names'''
if attribute not in attribute_names:
return None
else:
i = attribute_names.index(attribute)
return instance[i] # using the parameter name here
A function call starts with the function name, followed by a list of 0 or more comma-delimited arguments (aka 'actual parameters') enclosed within parentheses. A function call can be used as a statement or within an expression.
attribute = 'cap-shape' # try substituting any of the other attribute names shown above
print(attribute, '=', attribute_value(single_instance_list, 'cap-shape', attribute_names))
cap-shape = k
Note that Python does not distinguish between names used for variables and names used for functions. An assignment statement binds a value to a name; a function definition also binds a value to a name. At any given time, the value most recently bound to a name is the one that is used.
This can be demonstrated using the type(object) function, which returns the type of object.
x = 0
print('x used as a variable:', x, type(x))
def x():
print('x')
print('x used as a function:', x, type(x))
x used as a variable: 0 <type 'int'> x used as a function: <function x at 0x1049ae488> <type 'function'>
Another way to determine the type of an object is to use isinstance(object, class). This is generally preferable, as it takes into account class inheritance. There is a larger issue of duck typing, and whether code should ever explicitly check for the type of an object, but we will omit further discussion of the topic in this primer.
Call by sharing¶
An important feature of Python functions is that arguments are passed using call by sharing.
If a mutable object is passed as an argument to a function parameter, assignment statements using that parameter do not affect the passed argument, however other modifications to the parameter (e.g., modifications to a list using methods such as append(), remove(), reverse() or sort()) do affect the passed argument.
Not being aware of - or forgetting - this important distinction can lead to challenging debugging sessions.
The example below demonstrates this difference and introduces another list method, list.insert(i, x), which inserts x into list at position i.
def modify_parameters(parameter1, parameter2):
'''Inserts "x" at the head of parameter1, assigns [7, 8, 9] to parameter2'''
parameter1.insert(0, 'x') # insert() WILL affect argument passed as parameter1
print('parameter1, after inserting "x":', parameter1)
parameter2 = [7, 8, 9] # assignment WILL NOT affect argument passed as parameter2
print('parameter2, after assigning "x"', parameter2)
return
argument1 = [1, 2, 3]
argument2 = [4, 5, 6]
print('argument1, before calling modify_parameters:', argument1)
print('argument2, before calling modify_parameters:', argument2)
print()
modify_parameters(argument1, argument2)
print()
print('argument1, after calling modify_parameters:', argument1)
print('argument2, after calling modify_parameters:', argument2)
argument1, before calling modify_parameters: [1, 2, 3] argument2, before calling modify_parameters: [4, 5, 6] parameter1, after inserting "x": ['x', 1, 2, 3] parameter2, after assigning "x" [7, 8, 9] argument1, after calling modify_parameters: ['x', 1, 2, 3] argument2, after calling modify_parameters: [4, 5, 6]
One way of preventing functions from modifying mutable objects passed as parameters is to make a copy of those objects inside the function. Here is another version of the function above that makes a shallow copy of the list_parameter using the slice operator.
[Note: the Python copy module provides both [shallow] copy() and deepcopy() methods; we will cover modules further below.]
def modify_parameter_copy(parameter_1):
'''Inserts "x" at the head of parameter_1, without modifying the list argument'''
parameter_1_copy = parameter_1[:] # list[:] returns a copy of list
parameter_1_copy.insert(0, 'x')
print('Inserted "x":', parameter_1_copy)
return
argument_1 = [1, 2, 3] # passing a named object will not affect the object bound to that name
print('Before:', argument_1)
modify_parameter_copy(argument_1)
print('After:', argument_1)
Before: [1, 2, 3] Inserted "x": ['x', 1, 2, 3] After: [1, 2, 3]
Another way to avoid modifying parameters is to use assignment statements which do not modify the parameter objects but return a new object that is bound to the name (locally).
def modify_parameter_assignment(parameter_1):
'''Inserts "x" at the head of parameter_1, without modifying the list argument'''
parameter_1 = ['x'] + parameter_1 # using assignment rather than list.insert()
print('Inserted "x":', parameter_1)
return
argument_1 = [1, 2, 3] # passing a named object will not affect the object bound to that name
print('Before:', argument_1)
modify_parameter_assignment(argument_1)
print('After:', argument_1)
Before: [1, 2, 3] Inserted "x": ['x', 1, 2, 3] After: [1, 2, 3]
Multiple return values¶
Python functions can return more than one value by separating those return values with commas in the return statement. Multiple values are returned as a tuple.
If the function-invoking expression is an assignment statement, multiple variables can be assigned the multiple values returned by the function in a single statement. This combining of values and subsequent separation is known as tuple *packing* and *unpacking*.
def min_and_max(list_of_values):
'''Returns a tuple containing the min and max values in the list_of_values'''
return min(list_of_values), max(list_of_values)
list_1 = [3, 1, 4, 2, 5]
print('min and max of', list_1, ':', min_and_max(list_1))
# a single variable is assigned the two-element tuple
min_and_max_list_1 = min_and_max(list_1)
print('min and max of', list_1, ':', min_and_max_list_1)
# the 1st variable is assigned the 1st value, the 2nd variable is assigned the 2nd value
min_list_1, max_list_1 = min_and_max(list_1)
print('min and max of', list_1, ':', min_list_1, ',', max_list_1)
min and max of [3, 1, 4, 2, 5] : (1, 5) min and max of [3, 1, 4, 2, 5] : (1, 5) min and max of [3, 1, 4, 2, 5] : 1 , 5
Iteration: for, range¶
for i in [0, 1, 2]:
print(i)
0 1 2
for c in 'abc':
print(c)
a b c
The value of the variable used to iterate in a for statement persists after the for statement
i, c
(2, 'c')
In Python 2, the range(stop) function returns a list of values from 0 up to stop - 1 (inclusive). It is often used in the context of a for loop that iterates over the list of values.
print('Values for the', len(attribute_names), 'attributes:', end='\n\n') # adds a blank line
for i in range(len(attribute_names)):
print(attribute_names[i], '=',
attribute_value(single_instance_list, attribute_names[i], attribute_names))
Values for the 23 attributes: class = p cap-shape = k cap-surface = f cap-color = n bruises? = f odor = n gill-attachment = f gill-spacing = c gill-size = n gill-color = w stalk-shape = e stalk-root = ? stalk-surface-above-ring = k stalk-surface-below-ring = y stalk-color-above-ring = w stalk-color-below-ring = n veil-type = p veil-color = w ring-number = o ring-type = e spore-print-color = w population = v habitat = d
The more general form of the function, range(start, stop[, step]), returns a list of values from start to stop - 1 (inclusive) increasing by step (which defaults to 1), or from start down to stop + 1 (inclusive) decreasing by step if step is negative.
for i in range(3, 0, -1):
print(i)
3 2 1
In Python 2, the xrange(stop[, stop[, step]]) function is an iterable version of the range() function. In the context of a for loop, it returns the next item of the sequence for each iteration of the loop rather than creating all the elements of the sequence before the first iteration. This can reduce memory consumption in cases where iteration over all the items is not required.
In Python 3, the range() function behaves the same way as the xrange() function does in Python 2, and so the xrange() function is not defined in Python 3.
To maximize compatibility, we will use range() throughout this notebook; however, note that it is generally more efficient to use xrange() rather than range() in Python 2.
Modules, namespaces and dotted notation¶
A Python *module* is a file containing related definitions (e.g., of functions and variables). Modules are used to help organize a Python *namespace*, the set of identifiers accessible in a particular context. All of the functions and variables we define in this IPython Notebook are in the __main__ namespace, so accessing them does not require any specification of a module.
A Python module named simple_ml (in the file simple_ml.py), contains a set of solutions to the exercises in this IPython Notebook. [The learning opportunity provided by this primer will be maximized by not looking at that file, or waiting as long as possible to do so.]
Accessing functions in an external module requires that we first import the module, and then prefix the function names with the module name followed by a dot (this is known as *dotted notation*).
For example, the following function call in Exercise 1 below:
simple_ml.print_attribute_names_and_values(single_instance_list, attribute_names)
uses dotted notation to reference the print_attribute_names_and_values() function in the simple_ml module.
After you have defined your own function for Exercise 1, you can test your function by deleting the simple_ml module specification, so that the statement becomes
print_attribute_names_and_values(single_instance_list, attribute_names)
This will reference the print_attribute_names_and_values() function in the current namespace (__main__), i.e., the top-level interpreter environment. The simple_ml.print_attribute_names_and_values() function will still be accessible in the simple_ml namespace by using the "simple_ml." prefix (so you can easily toggle back and forth between your own definition and that provided in the solutions file).
Exercise 1: define print_attribute_names_and_values()¶
Complete the following function definition, print_attribute_names_and_values(instance, attribute_names), so that it generates exactly the same output as the code above.
def print_attribute_names_and_values(instance, attribute_names):
'''Prints the attribute names and values for an instance'''
# your code here
return
import simple_ml # this module contains my solutions to exercises
# delete 'simple_ml.' in the function call below to test your function
simple_ml.print_attribute_names_and_values(single_instance_list, attribute_names)
print_attribute_names_and_values(single_instance_list, attribute_names)
Values for the 23 attributes: class = p cap-shape = k cap-surface = f cap-color = n bruises? = f odor = n gill-attachment = f gill-spacing = c gill-size = n gill-color = w stalk-shape = e stalk-root = ? stalk-surface-above-ring = k stalk-surface-below-ring = y stalk-color-above-ring = w stalk-color-below-ring = n veil-type = p veil-color = w ring-number = o ring-type = e spore-print-color = w population = v habitat = d
File I/O¶
Python file input and output is done through file objects. A file object is created with the open(name[, mode]) statement, where name is a string representing the name of the file, and mode is 'r' (read), 'w' (write) or 'a' (append); if no second argument is provided, the mode defaults to 'r'.
A common Python programming pattern for processing an input text file is to
openthe file using awithstatement (which will automaticallyclosethe file after the statements inside thewithblock have been executed)- iterate over each line in the file using a
forstatement
The following code creates a list of instances, where each instance is a list of attribute values (like instance_1_str above).
all_instances = [] # initialize instances to an empty list
data_filename = 'agaricus-lepiota.data'
with open(data_filename, 'r') as f:
for line in f: # 'line' will be bound to the next line in f in each for loop iteration
all_instances.append(line.strip().split(','))
print('Read', len(all_instances), 'instances from', data_filename)
# we don't want to print all the instances, so we'll just print the first one to verify
print('First instance:', all_instances[0])
Read 8124 instances from agaricus-lepiota.data First instance: ['p', 'x', 's', 'n', 't', 'p', 'f', 'c', 'n', 'k', 'e', 'e', 's', 's', 'w', 'w', 'p', 'w', 'o', 'p', 'k', 's', 'u']
Exercise 2: define load_instances()¶
Define a function, load_instances(filename), that returns a list of instances in a text file. The function definition is started for you below. The function should exhibit the same behavior as the code above.
def load_instances(filename):
'''Returns a list of instances stored in a file.
filename is expected to have a series of comma-separated attribute values per line, e.g.,
p,k,f,n,f,n,f,c,n,w,e,?,k,y,w,n,p,w,o,e,w,v,d
'''
instances = []
# your code goes here
return instances
data_filename = 'agaricus-lepiota.data'
# delete 'simple_ml.' in the function call below to test your function
all_instances_2 = simple_ml.load_instances(data_filename)
print('Read', len(all_instances_2), 'instances from', data_filename)
print('First instance:', all_instances_2[0])
Read 8124 instances from agaricus-lepiota.data First instance: ['p', 'x', 's', 'n', 't', 'p', 'f', 'c', 'n', 'k', 'e', 'e', 's', 's', 'w', 'w', 'p', 'w', 'o', 'p', 'k', 's', 'u']
Output can be written to a text file via the file.write(str) method.
As we saw earlier, the str.join(words) method returns a single str-delimited string containing each of the strings in the words list.
SQL and Hive database tables sometimes use a pipe ('|') delimiter to separate column values for each row when they are stored as flat files. The following code creates a new data file using pipes rather than commas to separate the attribute values.
To help maintain internal consistency, it is generally a good practice to define a variable such as DELIMITER or SEPARATOR, bind it to the intended delimiter string, and then use it as a named constant. The Python language does not support named constants, so the use of variables as named constants depends on conventions (e.g., using ALL-CAPS).
DELIMITER = '|'
print('Converting to {}-delimited strings, e.g.,'.format(DELIMITER),
DELIMITER.join(all_instances[0]))
datafile2 = 'agaricus-lepiota-2.data'
with open(datafile2, 'w') as f: # 'w' = open file for writing (output)
for instance in all_instances:
f.write(DELIMITER.join(instance) + '\n') # write each instance on a separate line
all_instances_3 = []
with open(datafile2, 'r') as f:
for line in f:
all_instances_3.append(line.strip().split(DELIMITER)) # note: changed ',' to '|'
print('Read', len(all_instances_3), 'instances from', datafile2)
print('First instance:', all_instances_3[0])
Converting to |-delimited strings, e.g., p|x|s|n|t|p|f|c|n|k|e|e|s|s|w|w|p|w|o|p|k|s|u Read 8124 instances from agaricus-lepiota-2.data First instance: ['p', 'x', 's', 'n', 't', 'p', 'f', 'c', 'n', 'k', 'e', 'e', 's', 's', 'w', 'w', 'p', 'w', 'o', 'p', 'k', 's', 'u']
List comprehensions¶
Python provides a powerful list comprehension construct to simplify the creation of a list by specifying a formula in a single expression.
Some programmers find list comprehensions confusing, and avoid their use. We won't rely on list comprehensions here, but we will offer several examples with and without list comprehensions to highlight the power of the construct.
One common use of list comprehensions is in the context of the str.join(words) method we saw earlier.
If we wanted to construct a pipe-delimited string containing elements of the list, we could use a for loop to iteratively add list elements and pipe delimiters to a string for all but the last element, and then manually add the last element.
# create pipe-delimited string without using list comprehension
DELIMITER = '|'
delimited_string = ''
token_list = ['a', 'b', 'c']
for token in token_list[:-1]: # add all but the last token + DELIMITER
delimited_string += token + DELIMITER
delimited_string += token_list[-1] # add the last token (with no trailing DELIMITER)
delimited_string
'a|b|c'
This process is much simpler using a list comprehension.
delimited_string = DELIMITER.join([token for token in token_list])
delimited_string
'a|b|c'
Missing values & "clean" instances¶
As noted in the initial description of the UCI mushroom set above, 2480 of the 8124 instances have missing attribute values (denoted by '?').
There are several techniques for dealing with instances that include missing attribute values, but to simplify things in the context of this primer - and following the example in the Data Science for Business book - we will simply ignore any such instances and restrict our focus to only the clean instances (with no missing values).
We could use several lines of code - with an if statement inside a for loop - to create a clean_instances list from the all_instances list. Or we could use a list comprehension that includes an if statement.
We will show both approaches to creating clean_instances below.
# version 1: using an if statement nested within a for statement
UNKNOWN_VALUE = '?'
clean_instances = []
for instance in all_instances:
if UNKNOWN_VALUE not in instance:
clean_instances.append(instance)
print(len(clean_instances), 'clean instances')
5644 clean instances
# version 2: using an equivalent list comprehension
clean_instances = [instance
for instance in all_instances
if UNKNOWN_VALUE not in instance]
print(len(clean_instances), 'clean instances')
5644 clean instances
Note that line breaks can be used before a for or if keyword in a list comprehension.
Dictionaries (dicts)¶
Although single character abbreviations of attribute values (e.g., 'x') allow for more compact data files, they are not as easy to understand by human readers as the longer attribute value descriptions (e.g., 'convex').
A Python dictionary (or dict) is an unordered, comma-delimited collection of *key: value* pairs, serving a siimilar function as a hash table or hashmap in other programming languages.
We could create a dictionary for the cap-type attribute values shown above:
bell=b, conical=c, convex=x, flat=f, knobbed=k, sunken=s
Since we will want to look up the value using the abbreviation (which is the representation of the value stored in the file), we will use the abbreviations as keys and the descriptions as values.
A Python dictionary can be created by specifying all key: value pairs (with colons separating each key and value), or by adding them iteratively. We will show the first method in the cell below, and use the second method in a subsequent cell.
Note that a value in a Python dictionary (dict) can be accessed by specifying its key using the general form dict[key] (or dict.get(key, [default]), which allows the specification of a default value to use if key is not in dict).
attribute_values_cap_type = {'b': 'bell',
'c': 'conical',
'x': 'convex',
'f': 'flat',
'k': 'knobbed',
's': 'sunken'}
attribute_value_abbrev = 'x'
print(attribute_value_abbrev, '=', attribute_values_cap_type[attribute_value_abbrev])
x = convex
A Python dictionary is an iterable container, so we can iterate over the keys in a dictionary using a for loop.
Note that since a dictionary is an unordered collection, the sequence of abbreviations and associated values is not guaranteed to appear in any particular order.
for attribute_value_abbrev in attribute_values_cap_type:
print(attribute_value_abbrev, '=', attribute_values_cap_type[attribute_value_abbrev])
c = conical b = bell f = flat k = knobbed s = sunken x = convex
Python supports dictionary comprehensions, which have a similar form as the list comprehensions described above, except that both a key and a value have to be specified for each iteration.
For example, if we provisionally omit the 'convex' cap-type (whose abbreviation is the last letter rather than first letter in the attribute name), we could construct a dictionary of abbreviations and descriptions using the following expression.
attribute_values_cap_type_2 = {x[0]: x
for x in ['bell', 'conical', 'flat', 'knobbed', 'sunken']}
print(attribute_values_cap_type_2)
{'s': 'sunken', 'c': 'conical', 'b': 'bell', 'k': 'knobbed', 'f': 'flat'}
attribute_values_cap_type_2 = [[x[0], x ]
for x in ['bell', 'conical', 'flat', 'knobbed', 'sunken']]
print(attribute_values_cap_type_2)
[['b', 'bell'], ['c', 'conical'], ['f', 'flat'], ['k', 'knobbed'], ['s', 'sunken']]
While it's useful to have a dictionary of values for the cap-type attribute, it would be even more useful to have a dictionary of values for every attribute. Earlier, we created a list of attribute_names; we will now expand this to create a list of attribute_values wherein each list element is a dictionary.
Rather than explicitly type in each dictionary entry in the Python interpreter, we'll define a function to read a file containing the list of attribute names, values and value abbreviations in the format shown above:
- class: edible=e, poisonous=p
- cap-shape: bell=b, conical=c, convex=x, flat=f, knobbed=k, sunken=s
- cap-surface: fibrous=f, grooves=g, scaly=y, smooth=s
- ...
We can make calls to shell commands from a Python cell by using the bang (exclamation point). [There are a large number of cell magics that extend the capability of IPython Notebooks (which we will not explore further in this notebook.]
For example, the following cell will show the contents of the agaricus-lepiota.attributes file on OSX or Linux (for Windows, substitute type for cat).
! cat agaricus-lepiota.attributes
class: edible=e, poisonous=p cap-shape: bell=b, conical=c, convex=x, flat=f, knobbed=k, sunken=s cap-surface: fibrous=f, grooves=g, scaly=y, smooth=s cap-color: brown=n ,buff=b, cinnamon=c, gray=g, green=r, pink=p, purple=u, red=e, white=w, yellow=y bruises?: bruises=t, no=f odor: almond=a, anise=l, creosote=c, fishy=y, foul=f, musty=m, none=n, pungent=p, spicy=s gill-attachment: attached=a, descending=d, free=f, notched=n gill-spacing: close=c, crowded=w, distant=d gill-size: broad=b, narrow=n gill-color: black=k, brown=n, buff=b, chocolate=h, gray=g, green=r, orange=o, pink=p, purple=u, red=e, white=w, yellow=y stalk-shape: enlarging=e, tapering=t stalk-root: bulbous=b, club=c, cup=u, equal=e, rhizomorphs=z, rooted=r, missing=? stalk-surface-above-ring: fibrous=f, scaly=y, silky=k, smooth=s stalk-surface-below-ring: fibrous=f, scaly=y, silky=k, smooth=s stalk-color-above-ring: brown=n, buff=b, cinnamon=c, gray=g, orange=o, pink=p, red=e, white=w, yellow=y stalk-color-below-ring: brown=n, buff=b, cinnamon=c, gray=g, orange=o, pink=p, red=e, white=w, yellow=y veil-type: partial=p, universal=u veil-color: brown=n, orange=o, white=w, yellow=y ring-number: none=n, one=o, two=t ring-type: cobwebby=c, evanescent=e, flaring=f, large=l, none=n, pendant=p, sheathing=s, zone=z spore-print-color: black=k, brown=n, buff=b, chocolate=h, green=r, orange=o, purple=u, white=w, yellow=y population: abundant=a, clustered=c, numerous=n, scattered=s, several=v, solitary=y habitat: grasses=g, leaves=l, meadows=m, paths=p, urban=u, waste=w, woods=d
Exercise 3: define load_attribute_values()¶
We earlier created the attribute_names list manually. The load_attribute_values() function above creates the attribute_values list from the contents of a file, each line of which starts with the name of an attribute. Unfortunately, the function discards the name of each attribute.
It would be nice to retain the name as well as the value abbreviations and descriptions. One way to do this would be to create a list of dictionaries, in which each dictionary has 2 keys, a name, the value of which is the attribute name (a string), and values, the value of which is yet another dictionary (with abbreviation keys and description values, as in load_attribute_values()).
Complete the following function definition so that the code implements this functionality.
def load_attribute_names_and_values(filename):
'''Returns a list of attribute names and values in a file.
This list contains dictionaries wherein the keys are names
and the values are value description dictionariess.
Each value description sub-dictionary will use
the attribute value abbreviations as its keys
and the attribute descriptions as the values.
filename is expected to have one attribute name and set of values per line,
with the following format:
name: value_description=value_abbreviation[,value_description=value_abbreviation]*
for example
cap-shape: bell=b, conical=c, convex=x, flat=f, knobbed=k, sunken=s
The attribute name and values dictionary created from this line would be the following:
{'name': 'cap-shape',
'values': {'c': 'conical',
'b': 'bell',
'f': 'flat',
'k': 'knobbed',
's': 'sunken',
'x': 'convex'}}
'''
attribute_names_and_values = [] # this will be a list of dicts
# your code goes here
return attribute_names_and_values
attribute_filename = 'agaricus-lepiota.attributes'
# delete 'simple_ml.' in the function call below to test your function
attribute_names_and_values = simple_ml.load_attribute_names_and_values(attribute_filename)
print('Read', len(attribute_names_and_values), 'attribute values from', attribute_filename)
print('First attribute name:', attribute_names_and_values[0]['name'],
'; values:', attribute_names_and_values[0]['values'])
Read 23 attribute values from agaricus-lepiota.attributes
First attribute name: class ; values: {'p': 'poisonous', 'e': 'edible'}
Counters¶
Data scientists often need to count things. For example, we might want to count the numbers of edible and poisonous mushrooms in the clean_instances list we created earlier.
edible_count = 0
for instance in clean_instances:
if instance[0] == 'e':
edible_count += 1 # this is shorthand for edible_count = edible_count + 1
print('There are', edible_count, 'edible mushrooms among the',
len(clean_instances), 'clean instances')
There are 3488 edible mushrooms among the 5644 clean instances
More generally, we often want to count the number of occurrences (frequencies) of each possible value for an attribute. One way to do so is to create a dictionary where each dictionary key is an attribute value and each dictionary value is the count of instances with that attribute value.
Using an ordinary dictionary, we must be careful to create a new dictionary entry the first time we see a new attribute value (that is not already contained in the dictionary).
cap_state_value_counts = {}
for instance in clean_instances:
cap_state_value = instance[1] # cap-state is the 2nd attribute
if cap_state_value not in cap_state_value_counts:
# first occurrence, must explicitly initialize counter for this cap_state_value
cap_state_value_counts[cap_state_value] = 0
cap_state_value_counts[cap_state_value] += 1
print('Counts for each value of cap-state:')
for value in cap_state_value_counts:
print(value, ':', cap_state_value_counts[value])
Counts for each value of cap-state: c : 4 b : 300 f : 2432 k : 36 s : 32 x : 2840
The Python collections module provides a number of high performance container datatypes. A frequently useful datatype is a Counter, a specialized dictionary in which each key is a unique element found in a list or some other container, and each value is the number of occurrences of that element in the source container. The default value for each newly created key is zero.
A Counter includes a method, most_common([n]), that returns a list of 2-element tuples representing the values and their associated counts for the most common n values in descending order of the counts; if n is omitted, the method returns all tuples.
Note that we can either use
import collections
and then use collections.Counter() in our code, or use
from collections import Counter
and then use Counter() (with no module specification) in our code.
from collections import Counter
cap_state_value_counts = Counter()
for instance in clean_instances:
cap_state_value = instance[1]
# no need to explicitly initialize counters for cap_state_value; all start at zero
cap_state_value_counts[cap_state_value] += 1
print('Counts for each value of cap-state:')
for value in cap_state_value_counts:
print(value, ':', cap_state_value_counts[value])
Counts for each value of cap-state: c : 4 b : 300 f : 2432 k : 36 s : 32 x : 2840
When a Counter object is instantiated with a list of items, it returns a dictionary-like container in which the keys are the unique items in the list, and the values are the counts of each unique item in that list.
counts = Counter(['a', 'b', 'c', 'a', 'b', 'a'])
print(counts)
print(counts.most_common())
Counter({'a': 3, 'b': 2, 'c': 1})
[('a', 3), ('b', 2), ('c', 1)]
This allows us to count the number of values for cap-state in a very compact way.
We can use a Counter initialized with a list comprehension to collect all the values of the 2nd attribute, cap-state.
The following shows the first 10 instances; the second element in each sublist is the value of cap-state or that instance.
print(clean_instances[:10])
[['p', 'x', 's', 'n', 't', 'p', 'f', 'c', 'n', 'k', 'e', 'e', 's', 's', 'w', 'w', 'p', 'w', 'o', 'p', 'k', 's', 'u'], ['e', 'x', 's', 'y', 't', 'a', 'f', 'c', 'b', 'k', 'e', 'c', 's', 's', 'w', 'w', 'p', 'w', 'o', 'p', 'n', 'n', 'g'], ['e', 'b', 's', 'w', 't', 'l', 'f', 'c', 'b', 'n', 'e', 'c', 's', 's', 'w', 'w', 'p', 'w', 'o', 'p', 'n', 'n', 'm'], ['p', 'x', 'y', 'w', 't', 'p', 'f', 'c', 'n', 'n', 'e', 'e', 's', 's', 'w', 'w', 'p', 'w', 'o', 'p', 'k', 's', 'u'], ['e', 'x', 's', 'g', 'f', 'n', 'f', 'w', 'b', 'k', 't', 'e', 's', 's', 'w', 'w', 'p', 'w', 'o', 'e', 'n', 'a', 'g'], ['e', 'x', 'y', 'y', 't', 'a', 'f', 'c', 'b', 'n', 'e', 'c', 's', 's', 'w', 'w', 'p', 'w', 'o', 'p', 'k', 'n', 'g'], ['e', 'b', 's', 'w', 't', 'a', 'f', 'c', 'b', 'g', 'e', 'c', 's', 's', 'w', 'w', 'p', 'w', 'o', 'p', 'k', 'n', 'm'], ['e', 'b', 'y', 'w', 't', 'l', 'f', 'c', 'b', 'n', 'e', 'c', 's', 's', 'w', 'w', 'p', 'w', 'o', 'p', 'n', 's', 'm'], ['p', 'x', 'y', 'w', 't', 'p', 'f', 'c', 'n', 'p', 'e', 'e', 's', 's', 'w', 'w', 'p', 'w', 'o', 'p', 'k', 'v', 'g'], ['e', 'b', 's', 'y', 't', 'a', 'f', 'c', 'b', 'g', 'e', 'c', 's', 's', 'w', 'w', 'p', 'w', 'o', 'p', 'k', 's', 'm']]
The following list comprehension gathers the 2nd attribute of each of the first 10 sublists (note the slice notation).
[instance[1] for instance in clean_instances][:10]
['x', 'x', 'b', 'x', 'x', 'x', 'b', 'b', 'x', 'b']
Now we will gather all of the values for the 2nd attribute into a list and create a Counter for that list.
cap_state_value_counts = Counter([instance[1] for instance in clean_instances])
print('Counts for each value of cap-state:')
for value in cap_state_value_counts:
print(value, ':', cap_state_value_counts[value])
Counts for each value of cap-state: c : 4 b : 300 f : 2432 k : 36 s : 32 x : 2840
Exercise 4: define attribute_value_counts()¶
Define a function, attribute_value_counts(instances, attribute, attribute_names), that returns a Counter containing the counts of occurrences of each value of attribute in the list of instances. attribute_names is the list we created above, where each element is the name of an attribute.
This exercise is designed to generalize the solution shown in the code directly above (which handles only the cap-state attribute).
# your definition goes here
attribute = 'cap-shape'
# delete 'simple_ml.' in the function call below to test your function
attribute_value_counts = simple_ml.attribute_value_counts(clean_instances,
attribute,
attribute_names)
print('Counts for each value of', attribute, ':')
for value in attribute_value_counts:
print(value, ':', attribute_value_counts[value])
Counts for each value of cap-shape : c : 4 b : 300 f : 2432 k : 36 s : 32 x : 2840
More on sorting¶
Earlier, we saw that there is a list.sort() method that will sort a list in-place, i.e., by replacing the original value of list with a sorted version of the elements in list.
We also saw that the sorted(iterable[, cmp[, key[, reverse]]]) function can be used to return a copy of a list, dictionary or any other iterable container it is passed, in ascending order.
original_list = [3, 1, 4, 2, 5]
sorted_list = sorted(original_list)
print(original_list)
print(sorted_list)
[3, 1, 4, 2, 5] [1, 2, 3, 4, 5]
sorted() can also be used with dictionaries (it returns a sorted list of the dictionary keys).
print(sorted(attribute_values_cap_type))
['b', 'c', 'f', 'k', 's', 'x']
We can use the sorted keys to access the values of a dictionary in ascending order of the keys.
for attribute_value_abbrev in sorted(attribute_values_cap_type):
print(attribute_value_abbrev, '=', attribute_values_cap_type[attribute_value_abbrev])
b = bell c = conical f = flat k = knobbed s = sunken x = convex
attribute = 'cap-shape'
attribute_value_counts = simple_ml.attribute_value_counts(clean_instances,
attribute,
attribute_names)
print('Counts for each value of', attribute, ':')
for value in sorted(attribute_value_counts):
print(value, ':', attribute_value_counts[value])
Counts for each value of cap-shape : b : 300 c : 4 f : 2432 k : 36 s : 32 x : 2840
Sorting a dictionary by values¶
It is often useful to sort a dictionary by its values rather than its keys.
For example, when we printed out the counts of the attribute values for cap-shape above, the counts appeared in an ascending alphabetic order of their attribute names. It is often more helpful to show the attribute value counts in descending order of the counts (which are the values in that dictionary).
There are a variety of ways to sort a dictionary by values, but the approach described in PEP-256 is generally considered the most efficient.
In order to understand the components used in this approach, we will revisit and elaborate on a few concepts involving dictionaries, iterators and modules.
The dict.items() method returns an unordered list of (key, value) tuples in dict.
attribute_values_cap_type.items()
[('c', 'conical'),
('b', 'bell'),
('f', 'flat'),
('k', 'knobbed'),
('s', 'sunken'),
('x', 'convex')]
In Python 2, a related method, dict.iteritems(), returns an iterator: a callable object that returns the next item in a sequence each time it is referenced (e.g., during each iteration of a for loop), which can be more efficient than generating all the items in the sequence before any are used ... and so should be used rather than items() wherever possible
This is similar to the distinction between xrange() and range() described above ... and, also similarly, dict.items() is an iterator in Python 3 and so dict.iteritems() is no longer needed (nor defined) ... and further similarly, we will use only dict.items() in this notebook, but it is generally more efficient to use dict.iteritems() in Python 2.
for key, value in attribute_values_cap_type.items():
print(key, ':', value)
c : conical b : bell f : flat k : knobbed s : sunken x : convex
The Python operator module contains a number of functions that perform object comparisons, logical operations, mathematical operations, sequence operations, and abstract type tests.
To facilitate sorting a dictionary by values, we will use the operator.itemgetter(i) function that can be used to retrieve the ith value in a tuple (such as a (key, value) pair returned by [iter]items()).
We can use operator.itemgetter(1)) to reference the value - the 2nd item in each (key, value) tuple, (at zero-based index position 1) - rather than the key - the first item in each (key, value) tuple (at index position 0).
We will use the optional keyword argument key in sorted(iterable[, cmp[, key[, reverse]]]) to specify a sorting key that is not the same as the dict key (recall that the dict key is the default sorting key for sorted()).
import operator
sorted(attribute_values_cap_type.items(),
key=operator.itemgetter(1))
[('b', 'bell'),
('c', 'conical'),
('x', 'convex'),
('f', 'flat'),
('k', 'knobbed'),
('s', 'sunken')]
We can now sort the counts of attribute values in descending frequency of occurrence, and print them out using tuple unpacking.
attribute = 'cap-shape'
value_counts = simple_ml.attribute_value_counts(clean_instances,
attribute,
attribute_names)
print('Counts for each value of', attribute, '(sorted by count):')
for value, count in sorted(value_counts.items(),
key=operator.itemgetter(1),
reverse=True):
print(value, ':', count)
Counts for each value of cap-shape (sorted by count): x : 2840 f : 2432 b : 300 k : 36 s : 32 c : 4
Note that this example is rather contrived, as it is generally easiest to use a Counter and its associated most_common() method when sorting a dictionary wherein the values are all counts. The need to sort other kinds of dictionaries by their values is rather common.
String formatting¶
It is often helpful to use fancier output formatting than simply printing comma-delimited lists of items.
Examples of the str.format() function used in conjunction with print statements is shown below.
More details can be found in the Python documentation on format string syntax.
print('{:5.3f}'.format(0.1)) # fieldwidth = 5; precision = 3; f = float
print('{:7.3f}'.format(0.1)) # if fieldwidth is larger than needed, left pad with spaces
print('{:07.3f}'.format(0.1)) # use leading zero to left pad with leading zeros
print('{:3d}'.format(1)) # d = int
print('{:03d}'.format(1))
print('{:10s}'.format('hello')) # s = string, left-justified
print('{:>10s}'.format('hello')) # use '>' to right-justify within fieldwidth
0.100
0.100
000.100
1
001
hello
hello
The following example illustrates the use of str.format() on data associated with the mushroom dataset.
print('class: {} = {} ({:5.3f}), {} = {} ({:5.3f})'.format(
'e', 3488, 3488 / 5644,
'p', 2156, 2156 / 5644), end=' ')
class: e = 3488 (0.618), p = 2156 (0.382)
The following variation - splitting off the printing of the attribute name from the printing of the values and counts of values for that attrbiute - may be more useful in developing a solution to the following exercise.
print('class:', end=' ') # keeps cursor on the same line for subsequent print statements
print('{} = {} ({:5.3f}),'.format('e', 3488, 3488 / 5644), end=' ')
print('{} = {} ({:5.3f})'.format('p', 2156, 2156 / 5644), end=' ')
print() # advance the cursor to the beginning of the next line
class: e = 3488 (0.618), p = 2156 (0.382)
Exercise 5: define print_all_attribute_value_counts()¶
Define a function, print_all_attribute_value_counts(instances, attribute_names), that prints each attribute name in attribute_names, and then for each attribute value, prints the value abbreviation, the count of occurrences of that value and the proportion of instances that have that attribute value.
# your function definition goes here
print('\nCounts for all attributes and values:\n')
# delete 'simple_ml.' in the function call below to test your function
simple_ml.print_all_attribute_value_counts(clean_instances, attribute_names)
Counts for all attributes and values: class: e = 3488 (0.618), p = 2156 (0.382), cap-shape: x = 2840 (0.503), f = 2432 (0.431), b = 300 (0.053), k = 36 (0.006), s = 32 (0.006), c = 4 (0.001), cap-surface: y = 2220 (0.393), f = 2160 (0.383), s = 1260 (0.223), g = 4 (0.001), cap-color: g = 1696 (0.300), n = 1164 (0.206), y = 1056 (0.187), w = 880 (0.156), e = 588 (0.104), b = 120 (0.021), p = 96 (0.017), c = 44 (0.008), bruises?: t = 3184 (0.564), f = 2460 (0.436), odor: n = 2776 (0.492), f = 1584 (0.281), a = 400 (0.071), l = 400 (0.071), p = 256 (0.045), c = 192 (0.034), m = 36 (0.006), gill-attachment: f = 5626 (0.997), a = 18 (0.003), gill-spacing: c = 4620 (0.819), w = 1024 (0.181), gill-size: b = 4940 (0.875), n = 704 (0.125), gill-color: p = 1384 (0.245), n = 984 (0.174), w = 966 (0.171), h = 720 (0.128), g = 656 (0.116), u = 480 (0.085), k = 408 (0.072), r = 24 (0.004), y = 22 (0.004), stalk-shape: t = 2880 (0.510), e = 2764 (0.490), stalk-root: b = 3776 (0.669), e = 1120 (0.198), c = 556 (0.099), r = 192 (0.034), stalk-surface-above-ring: s = 3736 (0.662), k = 1332 (0.236), f = 552 (0.098), y = 24 (0.004), stalk-surface-below-ring: s = 3544 (0.628), k = 1296 (0.230), f = 552 (0.098), y = 252 (0.045), stalk-color-above-ring: w = 3136 (0.556), p = 1008 (0.179), g = 576 (0.102), n = 448 (0.079), b = 432 (0.077), c = 36 (0.006), y = 8 (0.001), stalk-color-below-ring: w = 3088 (0.547), p = 1008 (0.179), g = 576 (0.102), n = 496 (0.088), b = 432 (0.077), c = 36 (0.006), y = 8 (0.001), veil-type: p = 5644 (1.000), veil-color: w = 5636 (0.999), y = 8 (0.001), ring-number: o = 5488 (0.972), t = 120 (0.021), n = 36 (0.006), ring-type: p = 3488 (0.618), l = 1296 (0.230), e = 824 (0.146), n = 36 (0.006), spore-print-color: n = 1920 (0.340), k = 1872 (0.332), h = 1584 (0.281), w = 148 (0.026), r = 72 (0.013), u = 48 (0.009), population: v = 2160 (0.383), y = 1688 (0.299), s = 1104 (0.196), a = 384 (0.068), n = 256 (0.045), c = 52 (0.009), habitat: d = 2492 (0.442), g = 1860 (0.330), p = 568 (0.101), u = 368 (0.065), m = 292 (0.052), l = 64 (0.011),
4. Using Python to Build and Use a Simple Decision Tree Classifier¶
Decision Trees¶
Wikipedia offers the following description of a decision tree (with italics added to emphasize terms that will be elaborated below):
A decision tree is a flowchart-like structure in which each internal node represents a test of an attribute, each branch represents an outcome of that test and each leaf node represents class label (a decision taken after testing all attributes in the path from the root to the leaf). Each path from the root to a leaf can also be represented as a classification rule.
[Decision trees can also be used for regression, wherein the goal is to predict a continuous value rather than a class label, but we will focus here solely on their use for classification.]
The image below depicts a decision tree created from the UCI mushroom dataset that appears on Andy G's blog post about Decision Tree Learning, where
- a white box represents an internal node (and the label represents the attribute being tested)
- a blue box represents an attribute value (an outcome of the test of that attribute)
- a green box represents a leaf node with a class label of edible
- a red box represents a leaf node with a class label of poisonous

It is important to note that the UCI mushroom dataset consists entirely of categorical variables, i.e., every variable (or attribute) has an enumerated set of possible values. Many datasets include numeric variables that can take on int or float values. Tests for such variables typically use comparison operators, e.g., $age < 65$ or $36,250 < adjusted\_gross\_income <= 87,850$. [Aside: Python supports boolean expressions containing multiple comparison operators, such as the expression comparing adjusted_gross_income in the preceding example.]
Our simple decision tree will only accommodate categorical variables. We will closely follow a version of the decision tree learning algorithm implementation offered by Chris Roach.
Our goal in the following sections is to use Python to
- *create* a simple decision tree using a set of training instances
- *classify* (predict class labels) for a set of test instances using a simple decision tree
- *evaluate* the performance of a simple decision tree on classifying a set of test instances
First, we will explore some concepts and algorithms used in building and using decision trees.
Entropy¶
When building a supervised classification model, the frequency distribution of attribute values is a potentially important factor in determining the relative importance of each attribute at various stages in the model building process.
In data modeling, we can use frequency distributions to compute *entropy*, a measure of disorder (impurity) in a set.
We compute the entropy of multiplying the proportion of instances with each class label by the log of that proportion, and then taking the negative sum of those terms.
More precisely, for a 2-class (binary) classification task:
$entropy(S) = - p_1 log_2 (p_1) - p_2 log_2 (p_2)$
where $p_i$ is proportion (relative frequency) of class i within the set S.
From the output above, we know that the proportion of clean_instances that are labeled 'e' (class edible) in the UCI dataset is $3488 \div 5644 = 0.618$, and the proportion labeled 'p' (class poisonous) is $2156 \div 5644 = 0.382$.
After importing the Python math module, we can use the math.log(x[, base]) function in computing the entropy of the clean_instances of the UCI mushroom data set as follows.
import math
entropy = \
- (3488 / 5644) * math.log(3488 / 5644, 2) \
- (2156 / 5644) * math.log(2156 / 5644, 2)
print(entropy)
0.959441337353
Exercise 6: define entropy()¶
Define a function, entropy(instances), that computes the entropy of instances. You may assume the class label is in position 0; we will later see how to specify default parameter values in function definitions.
[Note: the class label in many data files is the last rather than the first item on each line.]
# your function definition here
# delete 'simple_ml.' in the function call below to test your function
print(simple_ml.entropy(clean_instances))
0.959441337353
Information Gain¶
Informally, a decision tree is constructed from a set of instances using a recursive algorithm that
- selects the best attribute
- splits the set into subsets based on the values of that attribute (each subset is composed of instances from the original set that have the same value for that attribute)
- repeats the process on each of these subsets until a stopping condition is met (e.g., a subset has no instances or has instances which all have the same class label)
Entropy is a metric that can be used in selecting the best attribute for each split: the best attribute is the one resulting in the largest decrease in entropy for a set of instances. [Note: other metrics can be used for determining the best attribute]
Information gain measures the decrease in entropy that results from splitting a set of instances based on an attribute.
$IG(S, a) = entropy(S) - [p(s_1) × entropy(s_1) + p(s_2) × entropy(s_2) ... + p(s_n) × entropy(s_n)]$
Where
- $n$ is the number of distinct values of attribute $a$
- $s_i$ is the subset of $S$ where all instances have the $i$th value of $a$
- $p(s_i)$ is the proportion of instances in $S$ that have the $i$th value of $a$
We'll use the definition of information_gain() in simple_ml to print the information gain for each of the attributes in the mushroom dataset ... before asking you to write your own definition of the function.
print('Information gain for different attributes:', end='\n\n')
for i in range(1, len(attribute_names)):
print('{:5.3f} {:2} {}'.format(
simple_ml.information_gain(clean_instances, i), i, attribute_names[i]))
Information gain for different attributes: 0.017 1 cap-shape 0.005 2 cap-surface 0.195 3 cap-color 0.140 4 bruises? 0.860 5 odor 0.004 6 gill-attachment 0.058 7 gill-spacing 0.032 8 gill-size 0.213 9 gill-color 0.275 10 stalk-shape 0.097 11 stalk-root 0.425 12 stalk-surface-above-ring 0.409 13 stalk-surface-below-ring 0.306 14 stalk-color-above-ring 0.279 15 stalk-color-below-ring 0.000 16 veil-type 0.002 17 veil-color 0.012 18 ring-number 0.463 19 ring-type 0.583 20 spore-print-color 0.110 21 population 0.101 22 habitat
We can sort the attributes based in decreasing order of information gain, which shows that odor is the best attribute for the first split in a decision tree that models the instances in this dataset.
print('Information gain for different attributes:', end='\n\n')
sorted_information_gain_indexes = sorted([(simple_ml.information_gain(clean_instances, i), i)
for i in range(1, len(attribute_names))],
reverse=True)
for gain, i in sorted_information_gain_indexes:
print('{:5.3f} {:2} {}'.format(gain, i, attribute_names[i]))
Information gain for different attributes: 0.860 5 odor 0.583 20 spore-print-color 0.463 19 ring-type 0.425 12 stalk-surface-above-ring 0.409 13 stalk-surface-below-ring 0.306 14 stalk-color-above-ring 0.279 15 stalk-color-below-ring 0.275 10 stalk-shape 0.213 9 gill-color 0.195 3 cap-color 0.140 4 bruises? 0.110 21 population 0.101 22 habitat 0.097 11 stalk-root 0.058 7 gill-spacing 0.032 8 gill-size 0.017 1 cap-shape 0.012 18 ring-number 0.005 2 cap-surface 0.004 6 gill-attachment 0.002 17 veil-color 0.000 16 veil-type
[The following variation does not use a list comprehension]
print('Information gain for different attributes:', end='\n\n')
information_gain_values = []
for i in range(1, len(attribute_names)):
information_gain_values.append((simple_ml.information_gain(clean_instances, i), i))
sorted_information_gain_indexes = sorted(information_gain_values,
reverse=True)
for gain, i in sorted_information_gain_indexes:
print('{:5.3f} {:2} {}'.format(gain, i, attribute_names[i]))
Information gain for different attributes: 0.860 5 odor 0.583 20 spore-print-color 0.463 19 ring-type 0.425 12 stalk-surface-above-ring 0.409 13 stalk-surface-below-ring 0.306 14 stalk-color-above-ring 0.279 15 stalk-color-below-ring 0.275 10 stalk-shape 0.213 9 gill-color 0.195 3 cap-color 0.140 4 bruises? 0.110 21 population 0.101 22 habitat 0.097 11 stalk-root 0.058 7 gill-spacing 0.032 8 gill-size 0.017 1 cap-shape 0.012 18 ring-number 0.005 2 cap-surface 0.004 6 gill-attachment 0.002 17 veil-color 0.000 16 veil-type
Exercise 7: define information_gain()¶
Define a function, information_gain(instances, i), that returns the information gain achieved by selecting the ith attribute to split instances. It should exhibit the same behavior as the simple_ml version of the function.
# your definition of information_gain(instances, i) here
# delete 'simple_ml.' in the function call below to test your function
sorted_information_gain_indexes = sorted([(simple_ml.information_gain(clean_instances, i), i)
for i in range(1, len(attribute_names))],
reverse=True)
print('Information gain for different attributes:', end='\n\n')
for gain, i in sorted_information_gain_indexes:
print('{:5.3f} {:2} {}'.format(gain, i, attribute_names[i]))
Information gain for different attributes: 0.860 5 odor 0.583 20 spore-print-color 0.463 19 ring-type 0.425 12 stalk-surface-above-ring 0.409 13 stalk-surface-below-ring 0.306 14 stalk-color-above-ring 0.279 15 stalk-color-below-ring 0.275 10 stalk-shape 0.213 9 gill-color 0.195 3 cap-color 0.140 4 bruises? 0.110 21 population 0.101 22 habitat 0.097 11 stalk-root 0.058 7 gill-spacing 0.032 8 gill-size 0.017 1 cap-shape 0.012 18 ring-number 0.005 2 cap-surface 0.004 6 gill-attachment 0.002 17 veil-color 0.000 16 veil-type
Building a Simple Decision Tree¶
We will implement a modified version of the ID3 algorithm for building a simple decision tree.
ID3 (Examples, Target_Attribute, Candidate_Attributes)
Create a Root node for the tree
If all examples have the same value of the Target_Attribute,
Return the single-node tree Root with label = that value
If the list of Candidate_Attributes is empty,
Return the single node tree Root,
with label = most common value of Target_Attribute in the examples.
Otherwise Begin
A ← The Attribute that best classifies examples (most information gain)
Decision Tree attribute for Root = A.
For each possible value, v_i, of A,
Add a new tree branch below Root, corresponding to the test A = v_i.
Let Examples(v_i) be the subset of examples that have the value v_i for A
If Examples(v_i) is empty,
Below this new branch add a leaf node
with label = most common target value in the examples
Else
Below this new branch add the subtree
ID3 (Examples(v_i), Target_Attribute, Attributes – {A})
End
Return Root
[Note:* the algorithm above is recursive, i.e., the there is a recursive call to ID3 within the definition of ID3. Covering recursion is beyond the scope of this primer, but there are a number of other resources on using recursion in Python. Familiarity with recursion will be important for understanding both the tree construction and classification functions below.]*
In building a decision tree, we will need to split the instances based on the index of the best attribute, i.e., the attribute that offers the highest information gain. We will use separate utility functions to handle these subtasks. To simplify the functions, we will rely exclusively on attribute indexes rather than attribute names.
First, we will define a function, split_instances(instances, attribute_index), to split a set of instances based on any attribute. This function will return a dictionary where each key is a distinct value of the specified attribute_index, and the value of each key is a list representing the subset of instances that have that attribute_index value.
We will use a defaultdict, a specialized dictionary class in the collections module, which automatically creates an appropriate default value for a new key. For example, a defaultdict(int) automatically initializes a new dictionary entry to 0 (zero); a defaultdict(list) automatically initializes a new dictionary entry to the empty list ([]).
from collections import defaultdict
def split_instances(instances, attribute_index):
'''Returns a list of dictionaries, splitting a list of instances
according to their values of a specified attribute index
The key of each dictionary is a distinct value of attribute_index,
and the value of each dictionary is a list representing
the subset of instances that have that value for the attribute
'''
partitions = defaultdict(list)
for instance in instances:
partitions[instance[attribute_index]].append(instance)
return partitions
To test the function, we will partition the clean_instances based on the odor attribute (index position 5) and print out the size (number of instances) in each partition rather than the lists of instances in each partition.
partitions = split_instances(clean_instances, 5)
print([(partition, len(partitions[partition])) for partition in partitions])
[('a', 400), ('c', 192), ('f', 1584), ('m', 36), ('l', 400), ('n', 2776), ('p', 256)]
Now that we can split instances based on a particular attribute, we would like to be able to choose the best attribute with which to split the instances, where best is defined as the attribute that provides the greatest information gain if instances were split based on that attribute. We will want to restrict the candidate attributes so that we don't bother trying to split on an attribute that was used higher up in the decision tree (or use the target attribute as a candidate).
Exercise 8: define choose_best_attribute_index()¶
Define a function, choose_best_attribute_index(instances, candidate_attribute_indexes), that returns the index in the list of candidate_attribute_indexes that provides the highest information gain if instances are split based on that attribute index.
# your function here
# delete 'simple_ml.' in the function call below to test your function
print('Best attribute index:',
simple_ml.choose_best_attribute_index(clean_instances, range(1, len(attribute_names))))
Best attribute index: 5
A leaf node in a decision tree represents the most frequently occurring - or majority - class value for that path through the tree. We will need a function that determines the majority value for the class index among a set of instances. One way to do this is to use the Counter class introduced above.
class_counts = Counter([instance[0] for instance in clean_instances])
print('class_counts: {}\n most_common(1): {}\n most_common(1)[0][0]: {}'.format(
class_counts, # the Counter object
class_counts.most_common(1), # returns a list in which the 1st element is a tuple with the most common value and its count
class_counts.most_common(1)[0][0])) # the most common value (1st element in that tuple)
class_counts: Counter({'e': 3488, 'p': 2156})
most_common(1): [('e', 3488)]
most_common(1)[0][0]: e
[The following variation does not use a list comprehension]
class_counts = Counter() # create an empty counter
for instance in clean_instances:
class_counts[instance[0]] += 1
print ('class_counts: {}\n most_common(1): {}\n most_common(1)[0][0]: {}'.format(
class_counts,
class_counts.most_common(1),
class_counts.most_common(1)[0][0]))
class_counts: Counter({'e': 3488, 'p': 2156})
most_common(1): [('e', 3488)]
most_common(1)[0][0]: e
It is often useful to compute the number of unique values and/or the total number of values in a Counter.
The number of unique values is simply the number of dictionary entries.
The total number of values can be computed by taking the sum() of all the counts (the value of each key: value pair ... or key, value tuple, if we use Counter().most_common()).
print('Number of unique values: {}'.format(len(class_counts)))
print('Total number of values: {}'.format(sum([v
for k, v in class_counts.most_common()])))
Number of unique values: 2 Total number of values: 5644
Before putting all this together to define a decision tree construction function, we will cover a few additional aspects of Python used in that function.
Truth values in Python¶
Python offers a very flexible mechanism for the testing of truth values: in an if condition, any null object, zero-valued numerical expression or empty container (string, list, dictionary or tuple) is interpreted as False (i.e., not True):
for x in [False, None, 0, 0.0, "", [], {}, ()]:
print('"{}" is'.format(x), end=' ')
if x:
print(True)
else:
print(False)
"False" is False
"None" is False
"0" is False
"0.0" is False
"" is False
"[]" is False
"{}" is False
"()" is False
Sometimes, particularly with function parameters, it is helpful to differentiate None from empty lists and other data structures with a False truth value (one common use case is illustrated in create_decision_tree() below).
for x in [False, None, 0, 0.0, "", [], {}, ()]:
print('"{} is None" is'.format(x), end=' ')
if x is None:
print(True)
else:
print(False)
"False is None" is False
"None is None" is True
"0 is None" is False
"0.0 is None" is False
" is None" is False
"[] is None" is False
"{} is None" is False
"() is None" is False
Conditional expressions (ternary operators)¶
Python also offers a conditional expression (ternary operator) that allows the functionality of an if/else statement that returns a value to be implemented as an expression. For example, the if/else statement in the code above could be implemented as a conditional expression as follows:
for x in [False, None, 0, 0.0, "", [], {}, ()]:
print('"{}" is {}'.format(x, True if x else False))
"False" is False
"None" is False
"0" is False
"0.0" is False
"" is False
"[]" is False
"{}" is False
"()" is False
More on optional parameters in Python functions¶
Python function definitions can specify default parameter values indicating the value those parameters will have if no argument is explicitly provided when the function is called. Arguments can also be passed using keyword parameters indicting which parameter will be assigned a specific argument value (which may or may not correspond to the order in which the parameters are defined).
The Python Tutorial page on default parameters includes the following warning:
Important warning: The default value is evaluated only once. This makes a difference when the default is a mutable object such as a list, dictionary, or instances of most classes.
Thus it is generally better to use the Python null object, None, rather than an empty list ([]), dict ({}) or other mutable data structure when specifying default parameter values for any of those data types.
def parameter_test(parameter1=None, parameter2=None):
'''Prints the values of parameter1 and parameter2'''
print('parameter1: {}; parameter2: {}'.format(parameter1, parameter2))
parameter_test() # no args are required
parameter_test(1) # if any args are provided, 1st arg gets assigned to parameter1
parameter_test(1, 2) # 2nd arg gets assigned to parameter2
parameter_test(2) # remember: if only 1 arg, 1st arg gets assigned to arg1
parameter_test(parameter2=2) # can use keyword to provide a value only for parameter2
parameter_test(parameter2=2, parameter1=1) # can use keywords for either arg, in either order
parameter1: None; parameter2: None parameter1: 1; parameter2: None parameter1: 1; parameter2: 2 parameter1: 2; parameter2: None parameter1: None; parameter2: 2 parameter1: 1; parameter2: 2
Exercise 9: define majority_value()¶
Define a function, majority_value(instances, class_index), that returns the most frequently occurring value of class_index in instances. The class_index parameter should be optional, and have a default value of 0 (zero).
Your function definition should support the use of optional arguments as used in the function calls below.
# your definition of majority_value(instances) here
# delete 'simple_ml.' in the function calls below to test your function
print('Majority value of index {}: {}'.format(
0, simple_ml.majority_value(clean_instances)))
# although there is only one class_index for the dataset,
# we'll test the function by specifying other indexes using optional / keyword arguments
print('Majority value of index {}: {}'.format(
1, simple_ml.majority_value(clean_instances, 1))) # using argument order
print('Majority value of index {}: {}'.format(
2, simple_ml.majority_value(clean_instances, class_index=2))) # using keyword argument
Majority value of index 0: e Majority value of index 1: x Majority value of index 2: y
Building a Simple Decision Tree¶
The recursive create_decision_tree() function below uses an optional parameter, class_index, which defaults to 0. This is to accommodate other datasets in which the class label is the last element on each line (which would be most easily specified by using a -1 value). Most data files in the UCI Machine Learning Repository have the class labels as either the first element or the last element.
To show how the decision tree is being built, an optional trace parameter, when non-zero, will generate some trace information as the tree is constructed. The indentation level is incremented with each recursive call via the use of the conditional expression (ternary operator), trace + 1 if trace else 0.
def create_decision_tree(instances,
candidate_attribute_indexes=None,
class_index=0,
default_class=None,
trace=0):
'''Returns a new decision tree trained on a list of instances.
The tree is constructed by recursively selecting and splitting instances based on
the highest information_gain of the candidate_attribute_indexes.
The class label is found in position class_index.
The default_class is the majority value for the current node's parent in the tree.
A positive (int) trace value will generate trace information
with increasing levels of indentation.
Derived from the simplified ID3 algorithm presented in Building Decision Trees in Python
by Christopher Roach,
http://www.onlamp.com/pub/a/python/2006/02/09/ai_decision_trees.html?page=3
'''
# if no candidate_attribute_indexes are provided,
# assume that we will use all but the target_attribute_index
# Note that None != [],
# as an empty candidate_attribute_indexes list is a recursion stopping condition
if candidate_attribute_indexes is None:
candidate_attribute_indexes = [i
for i in range(len(instances[0]))
if i != class_index]
# Note: do not use candidate_attribute_indexes.remove(class_index)
# as this would destructively modify the argument,
# causing problems during recursive calls
class_labels_and_counts = Counter([instance[class_index] for instance in instances])
# If the dataset is empty or the candidate attributes list is empty,
# return the default value
if not instances or not candidate_attribute_indexes:
if trace:
print('{}Using default class {}'.format('< ' * trace, default_class))
return default_class
# If all the instances have the same class label, return that class label
elif len(class_labels_and_counts) == 1:
class_label = class_labels_and_counts.most_common(1)[0][0]
if trace:
print('{}All {} instances have label {}'.format(
'< ' * trace, len(instances), class_label))
return class_label
else:
default_class = simple_ml.majority_value(instances, class_index)
# Choose the next best attribute index to best classify the instances
best_index = simple_ml.choose_best_attribute_index(
instances, candidate_attribute_indexes, class_index)
if trace:
print('{}Creating tree node for attribute index {}'.format(
'> ' * trace, best_index))
# Create a new decision tree node with the best attribute index
# and an empty dictionary object (for now)
tree = {best_index:{}}
# Create a new decision tree sub-node (branch) for each of the values
# in the best attribute field
partitions = simple_ml.split_instances(instances, best_index)
# Remove that attribute from the set of candidates for further splits
remaining_candidate_attribute_indexes = [i
for i in candidate_attribute_indexes
if i != best_index]
for attribute_value in partitions:
if trace:
print('{}Creating subtree for value {} ({}, {}, {}, {})'.format(
'> ' * trace,
attribute_value,
len(partitions[attribute_value]),
len(remaining_candidate_attribute_indexes),
class_index,
default_class))
# Create a subtree for each value of the the best attribute
subtree = create_decision_tree(
partitions[attribute_value],
remaining_candidate_attribute_indexes,
class_index,
default_class,
trace + 1 if trace else 0)
# Add the new subtree to the empty dictionary object
# in the new tree/node we just created
tree[best_index][attribute_value] = subtree
return tree
# split instances into separate training and testing sets
training_instances = clean_instances[:-20]
test_instances = clean_instances[-20:]
tree = create_decision_tree(training_instances, trace=1) # remove trace=1 to turn off tracing
print(tree)
> Creating tree node for attribute index 5
> Creating subtree for value a (400, 21, 0, e)
< < All 400 instances have label e
> Creating subtree for value c (192, 21, 0, e)
< < All 192 instances have label p
> Creating subtree for value f (1584, 21, 0, e)
< < All 1584 instances have label p
> Creating subtree for value m (28, 21, 0, e)
< < All 28 instances have label p
> Creating subtree for value l (400, 21, 0, e)
< < All 400 instances have label e
> Creating subtree for value n (2764, 21, 0, e)
> > Creating tree node for attribute index 20
> > Creating subtree for value k (1296, 20, 0, e)
< < < All 1296 instances have label e
> > Creating subtree for value r (72, 20, 0, e)
< < < All 72 instances have label p
> > Creating subtree for value w (100, 20, 0, e)
> > > Creating tree node for attribute index 21
> > > Creating subtree for value y (24, 19, 0, e)
< < < < All 24 instances have label e
> > > Creating subtree for value c (16, 19, 0, e)
< < < < All 16 instances have label p
> > > Creating subtree for value v (60, 19, 0, e)
< < < < All 60 instances have label e
> > Creating subtree for value n (1296, 20, 0, e)
< < < All 1296 instances have label e
> Creating subtree for value p (256, 21, 0, e)
< < All 256 instances have label p
{5: {'a': 'e', 'c': 'p', 'f': 'p', 'm': 'p', 'l': 'e', 'n': {20: {'k': 'e', 'r': 'p', 'w': {21: {'y': 'e', 'c': 'p', 'v': 'e'}}, 'n': 'e'}}, 'p': 'p'}}
The structure of the tree shown above is rather difficult to discern from the normal printed representation of a dictionary.
The Python pprint module has a number of useful methods for pretty-printing or formatting objects in a more human readable way.
The pprint.pprint(object, stream=None, indent=1, width=80, depth=None) method will print object to a stream (a default value of None will dictate the use of sys.stdout, the same destination as print function output), using indent spaces to differentiate nesting levels, using up to a maximum width columns and up to to a maximum nesting level depth (None indicating no maximum).
from pprint import pprint
pprint(tree)
{5: {'a': 'e',
'c': 'p',
'f': 'p',
'l': 'e',
'm': 'p',
'n': {20: {'k': 'e',
'n': 'e',
'r': 'p',
'w': {21: {'c': 'p', 'v': 'e', 'y': 'e'}}}},
'p': 'p'}}
Classifying Instances with a Simple Decision Tree¶
Usually, when we construct a decision tree based on a set of training instances, we do so with the intent of using that tree to classify a set of one or more test instances.
We will define a function, classify(tree, instance, default_class=None), to use a decision tree to classify a single instance, where an optional default_class can be specified as the return value if the instance represents a set of attribute values that don't have a representation in the decision tree.
We will use a design pattern in which we will use a series of if statements, each of which returns a value if the condition is true, rather than a nested series of if, elif and/or else clauses, as it helps constrain the levels of indentation in the function.
def classify(tree, instance, default_class=None):
'''Returns a classification label for instance, given a decision tree'''
if not tree: # if the node is empty, return the default class
return default_class
if not isinstance(tree, dict): # if the node is a leaf, return its class label
return tree
attribute_index = list(tree.keys())[0] # using list(dict.keys()) for Python 3 compatibility
attribute_values = list(tree.values())[0]
instance_attribute_value = instance[attribute_index]
if instance_attribute_value not in attribute_values: # this value was not in training data
return default_class
# recursively traverse the subtree (branch) associated with instance_attribute_value
return classify(attribute_values[instance_attribute_value], instance, default_class)
for instance in test_instances:
predicted_label = classify(tree, instance)
actual_label = instance[0]
print('predicted: {}; actual: {}'.format(predicted_label, actual_label))
predicted: p; actual: p predicted: p; actual: p predicted: p; actual: p predicted: e; actual: e predicted: e; actual: e predicted: p; actual: p predicted: e; actual: e predicted: e; actual: e predicted: e; actual: e predicted: p; actual: p predicted: e; actual: e predicted: e; actual: e predicted: e; actual: e predicted: p; actual: p predicted: e; actual: e predicted: e; actual: e predicted: e; actual: e predicted: e; actual: e predicted: p; actual: p predicted: p; actual: p
Evaluating the Accuracy of a Simple Decision Tree¶
It is often helpful to evaluate the performance of a model using a dataset not used in the training of that model. In the simple example shown above, we used all but the last 20 instances to train a simple decision tree, then classified those last 20 instances using the tree.
The advantage of this training/test split is that visual inspection of the classifications (sometimes called predictions) is relatively straightforward, revealing that all 20 instances were correctly classified.
There are a variety of metrics that can be used to evaluate the performance of a model. Scikit Learn's Model Evaluation library provides an overview and implementation of several possible metrics. For now, we'll simply measure the accuracy of a model, i.e., the percentage of test instances that are correctly classified (true positives and true negatives).
The accuracy of the model above, given the set of 20 test instances, is 100% (20/20).
The function below calculates the classification accuracy of a tree over a set of test_instances (with an optional class_index parameter indicating the position of the class label in each instance).
def classification_accuracy(tree, test_instances, class_index=0, default_class=None):
'''Returns the accuracy of classifying test_instances with tree,
where the class label is in position class_index'''
num_correct = 0
for i in range(len(test_instances)):
prediction = classify(tree, test_instances[i], default_class)
actual_value = test_instances[i][class_index]
if prediction == actual_value:
num_correct += 1
return num_correct / len(test_instances)
print(classification_accuracy(tree, test_instances))
1.0
In addition to showing the percentage of correctly classified instances, it may be helpful to return the actual counts of correctly and incorrectly classified instances, e.g., if we want to compile a total count of correctly and incorrectly classified instances over a collection of test instances.
In order to do so, we'll use the zip([iterable, ...]) function, which combines 2 or more sequences or iterables; the function returns a list of tuples, where the ith tuple contains the ith element from each of the argument sequences or iterables.
zip([0, 1, 2], ['a', 'b', 'c'])
[(0, 'a'), (1, 'b'), (2, 'c')]
We can use list comprehensions, the Counter class and the zip() function to modify classification_accuracy() so that it returns a packed tuple with
- the percentage of instances correctly classified
- the number of correctly classified instances
- the number of incorrectly classified instances
We'll also modify the function to use instances rather than test_instances, as we sometimes want to be able to valuate the accuracy of a model when tested on the training instances used to create it.
def classification_accuracy(tree, instances, class_index=0, default_class=None):
'''Returns the accuracy of classifying test_instances with tree,
where the class label is in position class_index'''
predicted_labels = [classify(tree, instance, default_class)
for instance in instances]
actual_labels = [x[class_index]
for x in instances]
counts = Counter([x == y
for x, y in zip(predicted_labels, actual_labels)])
return counts[True] / len(instances), counts[True], counts[False]
print(classification_accuracy(tree, test_instances))
(1.0, 20, 0)
We sometimes want to partition the instances into subsets of equal sizes to measure performance. One metric this partitioning allows us to compute is a learning curve, i.e., assess how well the model performs based on the size of its training set. Another use of these partitions (aka folds) would be to conduct an [n-fold cross validation](https://en.wikipedia.org/wiki/Cross-validation_(statistics) evaluation.
The following function, partition_instances(instances, num_partitions), partitions a set of instances into num_partitions relatively equally sized subsets.
We'll use this as yet another opportunity to demonstrate the power of using list comprehensions, this time, to condense the use of nested for loops.
def partition_instances(instances, num_partitions):
'''Returns a list of relatively equally sized disjoint sublists (partitions)
of the list of instances'''
return [[instances[j]
for j in range(i, len(instances), num_partitions)]
for i in range(num_partitions)]
Before testing this function on the 5644 clean_instances from the UCI mushroom dataset, we'll create a small number of simplified instances to verify that the function has the desired behavior.
instance_length = 3
num_instances = 5
simplified_instances = [[j
for j in range(i, instance_length + i)]
for i in range(num_instances)]
print('Instances:', simplified_instances)
partitions = partition_instances(simplified_instances, 2)
print('Partitions:', partitions)
Instances: [[0, 1, 2], [1, 2, 3], [2, 3, 4], [3, 4, 5], [4, 5, 6]] Partitions: [[[0, 1, 2], [2, 3, 4], [4, 5, 6]], [[1, 2, 3], [3, 4, 5]]]
[The following variations do not use list comprehensions]
def partition_instances(instances, num_partitions):
'''Returns a list of relatively equally sized disjoint sublists (partitions)
of the list of instances'''
partitions = []
for i in range(num_partitions):
partition = []
# iterate over instances starting at position i in increments of num_paritions
for j in range(i, len(instances), num_partitions):
partition.append(instances[j])
partitions.append(partition)
return partitions
simplified_instances = []
for i in range(num_instances):
new_instance = []
for j in range(i, instance_length + i):
new_instance.append(j)
simplified_instances.append(new_instance)
print('Instances:', simplified_instances)
partitions = partition_instances(simplified_instances, 2)
print('Partitions:', partitions)
Instances: [[0, 1, 2], [1, 2, 3], [2, 3, 4], [3, 4, 5], [4, 5, 6]] Partitions: [[[0, 1, 2], [2, 3, 4], [4, 5, 6]], [[1, 2, 3], [3, 4, 5]]]
The enumerate(sequence, start=0) function creates an iterator that successively returns the index and value of each element in a sequence, beginning at the start index.
for i, x in enumerate(['a', 'b', 'c']):
print(i, x)
0 a 1 b 2 c
We can use enumerate() to facilitate slightly more rigorous testing of our partition_instances function on our simplified_instances.
Note that since we are printing values rather than accumulating values, we will not use nested list comprehensions for this task.
for i in range(num_instances):
print('\n# partitions:', i)
for j, partition in enumerate(partition_instances(simplified_instances, i)):
print('partition {}: {}'.format(j, partition))
# partitions: 0 # partitions: 1 partition 0: [[0, 1, 2], [1, 2, 3], [2, 3, 4], [3, 4, 5], [4, 5, 6]] # partitions: 2 partition 0: [[0, 1, 2], [2, 3, 4], [4, 5, 6]] partition 1: [[1, 2, 3], [3, 4, 5]] # partitions: 3 partition 0: [[0, 1, 2], [3, 4, 5]] partition 1: [[1, 2, 3], [4, 5, 6]] partition 2: [[2, 3, 4]] # partitions: 4 partition 0: [[0, 1, 2], [4, 5, 6]] partition 1: [[1, 2, 3]] partition 2: [[2, 3, 4]] partition 3: [[3, 4, 5]]
Returning our attention to the UCI mushroom dataset, the following will partition our clean_instances into 10 relatively equally sized disjoint subsets. We will use a list comprehension to print out the length of each partition
partitions = partition_instances(clean_instances, 10)
print([len(partition) for partition in partitions])
[565, 565, 565, 565, 564, 564, 564, 564, 564, 564]
[The following variation does not use a list comprehension]
for partition in partitions:
print(len(partition), end=' ')
print()
565 565 565 565 564 564 564 564 564 564
The following shows the different trees that are constructed based on partition 0 (first 10th) of clean_instances, partitions 0 and 1 (first 2/10ths) of clean_instances and all clean_instances.
tree0 = create_decision_tree(partitions[0])
print('Tree trained with {} instances:'.format(len(partitions[0])))
pprint(tree0)
print()
tree1 = create_decision_tree(partitions[0] + partitions[1])
print('Tree trained with {} instances:'.format(len(partitions[0] + partitions[1])))
pprint(tree1)
print()
tree = create_decision_tree(clean_instances)
print('Tree trained with {} instances:'.format(len(clean_instances)))
pprint(tree)
Tree trained with 565 instances:
{5: {'a': 'e',
'c': 'p',
'f': 'p',
'l': 'e',
'm': 'p',
'n': {20: {'k': 'e', 'n': 'e', 'r': 'p', 'w': 'e'}},
'p': 'p'}}
Tree trained with 1130 instances:
{5: {'a': 'e',
'c': 'p',
'f': 'p',
'l': 'e',
'm': 'p',
'n': {20: {'k': 'e',
'n': 'e',
'r': 'p',
'w': {21: {'c': 'p', 'v': 'e', 'y': 'e'}}}},
'p': 'p'}}
Tree trained with 5644 instances:
{5: {'a': 'e',
'c': 'p',
'f': 'p',
'l': 'e',
'm': 'p',
'n': {20: {'k': 'e',
'n': 'e',
'r': 'p',
'w': {21: {'c': 'p', 'v': 'e', 'y': 'e'}}}},
'p': 'p'}}
The only difference between the first two trees - tree0 and tree1 - is that in the first tree, instances with no odor (attribute index 5 is 'n') and a spore-print-color of white (attribute 20 = 'w') are classified as edible ('e'). With additional training data in the 2nd partition, an additional distinction is made such that instances with no odor, a white spore-print-color and a clustered population (attribute 21 = 'c') are classified as poisonous ('p'), while all other instances with no odor and a white spore-print-color (and any other value for the population attribute) are classified as edible ('e').
Note that there is no difference between tree1 and tree (the tree trained with all instances). This early convergence on an optimal model is uncommon on most datasets (outside the UCI repository).
Learning curves¶
Now that we can partition our instances into subsets, we can use these subsets to construct different-sized training sets in the process of computing a learning curve.
We will start off with an initial training set consisting only of the first partition, and then progressively extend that training set by adding a new partition during each iteration of computing the learning curve.
The list.extend(L) method enables us to extend list by appending all the items in another list, L, to the end of list.
x = [1, 2, 3]
x.extend([4, 5])
print(x)
[1, 2, 3, 4, 5]
We can now define the function, compute_learning_curve(instances, num_partitions=10), which will take a list of instances, partition it into num_partitions relatively equally sized disjoint partitions, and then iteratively evaluate the accuracy of models trained with an incrementally increasing combination of instances in the first num_partitions - 1 partitions then tested with instances in the last partition, a variant of . That is, a model trained with the first partition will be constructed (and tested), then a model trained with the first 2 partitions will be constructed (and tested), and so on.
The function will return a list of num_partitions - 1 tuples representing the size of the training set and the accuracy of a tree trained with that set (and tested on the num_partitions - 1 set). This will provide some indication of the relative impact of the size of the training set on model performance.
def compute_learning_curve(instances, num_partitions=10):
'''Returns a list of training sizes and scores for incrementally increasing partitions.
The list contains 2-element tuples, each representing a training size and score.
The i-th training size is the number of instances in partitions 0 through num_partitions - 2.
The i-th score is the accuracy of a tree trained with instances
from partitions 0 through num_partitions - 2
and tested on instances from num_partitions - 1 (the last partition).'''
partitions = partition_instances(instances, num_partitions)
test_instances = partitions[-1][:]
training_instances = []
accuracy_list = []
for i in range(0, num_partitions - 1):
# for each iteration, the training set is composed of partitions 0 through i - 1
training_instances.extend(partitions[i][:])
tree = create_decision_tree(training_instances)
partition_accuracy = classification_accuracy(tree, test_instances)
accuracy_list.append((len(training_instances), partition_accuracy))
return accuracy_list
accuracy_list = compute_learning_curve(clean_instances)
print(accuracy_list)
[(565, (0.9964539007092199, 562, 2)), (1130, (1.0, 564, 0)), (1695, (1.0, 564, 0)), (2260, (1.0, 564, 0)), (2824, (1.0, 564, 0)), (3388, (1.0, 564, 0)), (3952, (1.0, 564, 0)), (4516, (1.0, 564, 0)), (5080, (1.0, 564, 0))]
The UCI mushroom dataset is a particularly clean and simple data set, enabling quick convergence on an optimal decision tree for classifying new instances using relatively few training instances.
We can use a larger number of smaller partitions to see a little more variation in accuracy performance.
accuracy_list = compute_learning_curve(clean_instances, 100)
print(accuracy_list[:10])
[(57, (0.9821428571428571, 55, 1)), (114, (1.0, 56, 0)), (171, (0.9821428571428571, 55, 1)), (228, (1.0, 56, 0)), (285, (1.0, 56, 0)), (342, (1.0, 56, 0)), (399, (1.0, 56, 0)), (456, (1.0, 56, 0)), (513, (1.0, 56, 0)), (570, (1.0, 56, 0))]
Object-Oriented Programming: Defining a Python Class to Encapsulate a Simple Decision Tree¶
The simple decision tree defined above uses a Python dictionary for its representation. One can imagine using other data structures, and/or extending the decision tree to support confidence estimates, numeric features and other capabilities that are often included in more fully functional implementations. To support future extensibility, and hide the details of the representation from the user, it would be helpful to have a user-defined class for simple decision trees.
Python is an object-oriented programming language, offering simple syntax and semantics for defining classes and instantiating objects of those classes. [It is assumed that the reader is already familiar with the concepts of object-oriented programming]
A Python class starts with the keyword class followed by a class name (identifier), a colon (':'), and then any number of statements, which typically take the form of assignment statements for class or instance variables and/or function definitions for class methods. All statements are indented to reflect their inclusion in the class definition.
The members - methods, class variables and instance variables - of a class are accessed by prepending self. to each reference. Class methods always include self as the first parameter.
All class members in Python are public (accessible outside the class). There is no mechanism for private class members, but identifiers with leading double underscores (__member_identifier) are 'mangled' (translated into _class_name__member_identifier), and thus not directly accessible outside their class, and can be used to approximate private members by Python programmers.
There is also no mechanism for protected identifiers - accessible only within a defining class and its subclasses - in the Python language, and so Python programmers have adopted the convention of using a single underscore (_identifier) at the start of any identifier that is intended to be protected (i.e., not to be accessed outside the class or its subclasses).
Some Python programmers only use the single underscore prefixes and avoid double underscore prefixes due to unintended consequences that can arise when names are mangled. The following warning about single and double underscore prefixes is issued in Code Like a Pythonista:
try to avoid the __private form. I never use it. Trust me. If you use it, you WILL regret it later
We will follow this advice and avoid using the double underscore prefix in user-defined member variables and methods.
Python has a number of pre-defined special method names, all of which are denoted by leading and trailing double underscores. For example, the object.__init__(self[, ...]) method is used to specify instructions that should be executed whenever a new object of a class is instantiated.
Note that other machine learning libraries may use different terminology for some of the functions we defined above. For example, in the sklearn.tree.DecisionTreeClassifier class (and in most sklearn classifier classes), the method for constructing a classifier is named fit() - since it "fits" the data to a model - and the method for classifying instances is named predict() - since it is predicting the class label for an instance.
In keeping with this common terminology, the code below defines a class, SimpleDecisionTree, with a single pseudo-protected member variable _tree, three public methods - fit(), predict() and pprint() - and two pseudo-protected auxilary methods - _create_tree() and _predict() - to augment the fit() and predict() methods, respectively.
The fit() method is identical to the create_decision_tree() function above, with the inclusion of the self parameter (as it is now a class method rather than a function). The predict() method is a similarly modified version of the classify() function, with the added capability to predict the label of either a single instance or a list of instances. The classification_accuracy() method is similar to the function of the same name (with the addition of the self parameter). The pprint() method prints the tree in a human-readable format.
Most comments and the use of the trace parameter have been removed to make the code more compact, but are included in the version found in simple_decision_tree.py.
class SimpleDecisionTree:
_tree = {} # this instance variable becomes accessible to class methods via self._tree
def __init__(self):
# this is where we would initialize any parameters to the SimpleDecisionTree
pass
def fit(self,
instances,
candidate_attribute_indexes=None,
target_attribute_index=0,
default_class=None):
if not candidate_attribute_indexes:
candidate_attribute_indexes = [i
for i in range(len(instances[0]))
if i != target_attribute_index]
self._tree = self._create_tree(instances,
candidate_attribute_indexes,
target_attribute_index,
default_class)
def _create_tree(self,
instances,
candidate_attribute_indexes,
target_attribute_index=0,
default_class=None):
class_labels_and_counts = Counter([instance[target_attribute_index]
for instance in instances])
if not instances or not candidate_attribute_indexes:
return default_class
elif len(class_labels_and_counts) == 1:
class_label = class_labels_and_counts.most_common(1)[0][0]
return class_label
else:
default_class = simple_ml.majority_value(instances, target_attribute_index)
best_index = simple_ml.choose_best_attribute_index(instances,
candidate_attribute_indexes,
target_attribute_index)
tree = {best_index:{}}
partitions = simple_ml.split_instances(instances, best_index)
remaining_candidate_attribute_indexes = [i
for i in candidate_attribute_indexes
if i != best_index]
for attribute_value in partitions:
subtree = self._create_tree(
partitions[attribute_value],
remaining_candidate_attribute_indexes,
target_attribute_index,
default_class)
tree[best_index][attribute_value] = subtree
return tree
def predict(self, instances, default_class=None):
if not isinstance(instances, list):
return self._predict(self._tree, instance, default_class)
else:
return [self._predict(self._tree, instance, default_class)
for instance in instances]
def _predict(self, tree, instance, default_class=None):
if not tree:
return default_class
if not isinstance(tree, dict):
return tree
attribute_index = list(tree.keys())[0] # using list(dict.keys()) for Py3 compatibiity
attribute_values = list(tree.values())[0]
instance_attribute_value = instance[attribute_index]
if instance_attribute_value not in attribute_values:
return default_class
return self._predict(attribute_values[instance_attribute_value],
instance,
default_class)
def classification_accuracy(self, instances, default_class=None):
predicted_labels = self.predict(instances, default_class)
actual_labels = [x[0] for x in instances]
counts = Counter([x == y for x, y in zip(predicted_labels, actual_labels)])
return counts[True] / len(instances), counts[True], counts[False]
def pprint(self):
pprint(self._tree)
The following statements instantiate a SimpleDecisionTree, using all but the last 20 clean_instances, prints out the tree using its pprint() method, and then uses the classify() method to print the classification of the last 20 clean_instances.
simple_decision_tree = SimpleDecisionTree()
simple_decision_tree.fit(training_instances)
simple_decision_tree.pprint()
print()
predicted_labels = simple_decision_tree.predict(test_instances)
actual_labels = [instance[0] for instance in test_instances]
for predicted_label, actual_label in zip(predicted_labels, actual_labels):
print('Model: {}; truth: {}'.format(predicted_label, actual_label))
print()
print('Classification accuracy:', simple_decision_tree.classification_accuracy(test_instances))
{5: {'a': 'e',
'c': 'p',
'f': 'p',
'l': 'e',
'm': 'p',
'n': {20: {'k': 'e',
'n': 'e',
'r': 'p',
'w': {21: {'c': 'p', 'v': 'e', 'y': 'e'}}}},
'p': 'p'}}
Model: p; truth: p
Model: p; truth: p
Model: p; truth: p
Model: e; truth: e
Model: e; truth: e
Model: p; truth: p
Model: e; truth: e
Model: e; truth: e
Model: e; truth: e
Model: p; truth: p
Model: e; truth: e
Model: e; truth: e
Model: e; truth: e
Model: p; truth: p
Model: e; truth: e
Model: e; truth: e
Model: e; truth: e
Model: e; truth: e
Model: p; truth: p
Model: p; truth: p
Classification accuracy: (1.0, 20, 0)
5. Next steps¶
There are a variety of Python libraries - e.g., Scikit-Learn - for building more full-featured decision trees and other types of models based on a variety of machine learning algorithms. Hopefully, this primer will have prepared you for learning how to use those libraries effectively.
Many Python-based machine learning libraries use other external Python libraries such as NumPy, SciPy, Matplotlib and pandas. There are tutorials available for each of these libraries, including the following:
- Tentative NumPy Tutorial
- SciPy Tutorial
- Matplotlib PyPlot Tutorial
- Pandas Tutorials (especially 10 Minutes to Pandas)
There are many machine learning or data science resources that may be useful to help you continue the journey. Here is a sampling:
- Scikit-learn's tutorial, An introduction to machine learning with scikit-learn
- Kevin Markham's video series (on the Kaggle blog), An introduction to machine learning with scikit-learn
- Kaggle's Getting Started With Python For Data Science
- Coursera's Introduction to Data Science
- Olivier Grisel's Strata 2014 tutorial, Parallel Machine Learning with scikit-learn and IPython
Please feel free to contact the author ([Joe McCarthy](mailto:joe@interrelativity.com?subject=Python for Data Science)) to suggest additional resources.