import numpy as np
%matplotlib inline
Shocktube: shock with specified Mach number¶
Here we set up a shock tube with specified right state
[ρr,ur=0,pr]and left velocity ul=0, such that the solution consists of a right-going shock wave moving at a prescribed Mach number M relative to the right ambient state:
s=Mcr.What we know in advance about the Riemann solution is depicted below.
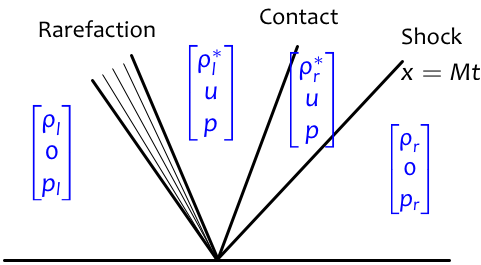
Let μ=2(M2−1)M(γ+1).
Using the Rankine-Hugoniot conditions, we find that the state just to the right of the contact is given by the following:
ρ∗r=ρrMM−μu=μcrp=pr(2M2−1)γ+1γ+1.Next, we know that the left state and the [ρ∗l,u,p] state must be connected by a left-going rarefaction. The relevant Riemann invariants imply
ρl=4γpl(γ−1)2u2(1−(ppl)γ−12γ)2and
ρ∗l=(ppl)1/γρl.So we can prescribe any value we like for pl and compute the remaining values ρl,ρ∗l from the equations above. The only catch is that the resulting rarefaction should satisfy the entropy condition, which is true if pl>p.
gamma = 1.4
M = 1.5
# Right state
rho_r = 1.0
u_r = 0.0 # This must be zero.
p_r = 1.0
# Left state
p_l = 5.0
u_l = 0.0 # This must be zero.
c_r = np.sqrt(gamma*p_r/rho_r) # Right state sound speed
s = M * c_r # Shock speed
mu = 2*(M**2-1)/(gamma+1)/M
# Find state to right of discontinuity via Rankine-Hugoniot conditions
p = p_r * ((2*M**2-1)*gamma+1)/(gamma+1)
u = mu*c_r
rho_rs = rho_r*M/(M-mu)
# Check that the 1-wave is a rarefaction
if p_l<p:
print "Warning: the states provided do not lead to the expected solution structure."
# Find remaining densities
rho_l = 4*gamma*p_l/((gamma-1)**2*u**2) * (1-(p/p_l)**((gamma-1)/(2*gamma)))**2
rho_ls= (p/p_l)**(1/gamma) * rho_l
from clawpack import pyclaw
from clawpack import riemann
from clawpack.riemann.euler_with_efix_1D_constants import density, momentum, energy, num_eqn
# Specify equations and boundary conditions
solver = pyclaw.ClawSolver1D(riemann.euler_with_efix_1D)
solver.bc_lower[0] = pyclaw.BC.extrap
solver.bc_upper[0] = pyclaw.BC.extrap
# Grid
x = pyclaw.Dimension('x',-1.,1.,1000)
domain = pyclaw.Domain([x])
state = pyclaw.State(domain,num_eqn)
state.problem_data['gamma'] = gamma
xc = state.grid.p_centers[0]
# Initial values
state.q[density,:] = rho_l*(xc<0) + rho_r*(xc>=0)
state.q[momentum,:] = rho_l*u_l*(xc<0) + rho_r*u_r*(xc>=0)
E_r = 0.5*rho_r * u_r**2 + p_r/(gamma-1)
E_l = 0.5*rho_l * u_l**2 + p_l/(gamma-1)
state.q[energy, :] = E_l*(xc<0) + E_r*(xc>=0)
claw = pyclaw.Controller()
claw.tfinal = 1.
claw.solution = pyclaw.Solution(state,domain)
claw.solver = solver
claw.num_output_times = 10
claw.keep_copy = True
claw.run()
2014-10-20 14:07:29,134 INFO CLAW: Solution 0 computed for time t=0.000000 2014-10-20 14:07:29,193 INFO CLAW: Solution 1 computed for time t=0.100000 2014-10-20 14:07:29,256 INFO CLAW: Solution 2 computed for time t=0.200000 2014-10-20 14:07:29,332 INFO CLAW: Solution 3 computed for time t=0.300000 2014-10-20 14:07:29,421 INFO CLAW: Solution 4 computed for time t=0.400000 2014-10-20 14:07:29,497 INFO CLAW: Solution 5 computed for time t=0.500000 2014-10-20 14:07:29,562 INFO CLAW: Solution 6 computed for time t=0.600000 2014-10-20 14:07:29,628 INFO CLAW: Solution 7 computed for time t=0.700000 2014-10-20 14:07:29,694 INFO CLAW: Solution 8 computed for time t=0.800000 2014-10-20 14:07:29,759 INFO CLAW: Solution 9 computed for time t=0.900000 2014-10-20 14:07:29,824 INFO CLAW: Solution 10 computed for time t=1.000000
{'cflmax': 0.953655319923049,
'dtmax': 0.0010564183672772706,
'dtmin': 0.0007603515077312271,
'numsteps': 1319}
from matplotlib import animation
from clawpack.visclaw.JSAnimation import IPython_display
import matplotlib.pyplot as plt
# Animated plot of the solution density
fig = plt.figure(figsize=[8,4])
ymax = max(rho_l, rho_ls, rho_rs, rho_r)
ax = plt.axes(xlim=(xc[0], xc[-1]), ylim=(0, ymax+0.5))
line, = ax.plot([], [], lw=1)
def fplot(i):
frame = claw.frames[i]
q = frame.q[0,:]
line.set_data(xc, q)
ax.set_title('Density at t= '+ str(frame.t))
return line,
animation.FuncAnimation(fig, fplot, frames=len(claw.frames))