#!/usr/bin/env python
# coding: utf-8
# # Constraint Satisfaction Problems (CSP) and Methods
#
# ## What is a Constraint Satisfaction Problem?
#
# Defined by
# * variables to which you must assign values,
# * valid values to assign to each variable,
# * constraints, or restrictions, on assigned values involving one or more variables
# * preferences among possible assignments, making it a Constraint Optimization Problem (COP).
#
# Many kinds of problems can be expressed as CSPs:
# * map coloring
# * job-shop scheduling
# * cryptarithmetic puzzles
# * puzzles like Sudoku, and eight-queens
#
# or COPs:
# * scheduling
# * packet-routing
# ## What is a Constraint Satisfaction Problem Solution Method?
#
# Well, it is a search!! :)
#
# Three approaches are described by our authors:
#
# - constraint propagation
# - Each state is list of valid values for each variable.
# - Next states are ones with different list of valid values.
#
#
# - backtracking search
# - Each state is a partial assignment---some variables have assigned values.
# - Next states are ones with an additional variable assigned.
#
#
# - local search
# - Each state is a complete assignment---all variables are assigned values.
# - Next states are complete assignments with value of one variable changed.
# ### Constraint Propagation
#
# Map coloring problem is a nice example.
#
#  #
# What are the variables? What are the domains of values for each
# variable?
#
# What are the constraints? No neighboring regions can have the same
# color. Can be expressed in a constraint graph with
# * nodes representing variables
# * edges representing pairwise (binary) constraints
#
#
#
# What are the variables? What are the domains of values for each
# variable?
#
# What are the constraints? No neighboring regions can have the same
# color. Can be expressed in a constraint graph with
# * nodes representing variables
# * edges representing pairwise (binary) constraints
#
#  #
# A popular constraint propagation algorithm is AC-3. "AC" is for
# "arc-consistency". 3 is for third version. It proceeds by removing
# values from the domains of variables at either end of an arc to
# maintain the constraints.
#
# A stronger version of this approach is called path-consistency (PC-2). It considers triplets of variables at a time.
#
# | | | WA | NT | SA | Q | NSW | V | T |
# | :--: | :--: | :--: | :--: | :--: | :--: | :--: | :--: | :--: |
# | 1 | | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | 2 | WA-NT considering SA | (r) | (g) | (b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (g) | (r) | (b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (g) | (r) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (r) | (g) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | 3 | NT-SA considering Q | (r) | (g) | (b) | (r) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (g) | (r) | (b) | (g) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (g) | (r) | (b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (r) | (g) | (b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | 4 | and so on ... |
# ### Backtracking Search
#
# Assign value to one variable at a time. Do depth-first search with backtracking.
#
#
#
# A popular constraint propagation algorithm is AC-3. "AC" is for
# "arc-consistency". 3 is for third version. It proceeds by removing
# values from the domains of variables at either end of an arc to
# maintain the constraints.
#
# A stronger version of this approach is called path-consistency (PC-2). It considers triplets of variables at a time.
#
# | | | WA | NT | SA | Q | NSW | V | T |
# | :--: | :--: | :--: | :--: | :--: | :--: | :--: | :--: | :--: |
# | 1 | | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | 2 | WA-NT considering SA | (r) | (g) | (b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (g) | (r) | (b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (g) | (r) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (r) | (g) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | 3 | NT-SA considering Q | (r) | (g) | (b) | (r) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (g) | (r) | (b) | (g) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (g) | (r) | (b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (r) | (g) | (b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | 4 | and so on ... |
# ### Backtracking Search
#
# Assign value to one variable at a time. Do depth-first search with backtracking.
#
#  #
#  #
#  #
#
# Many ideas exist for guiding the depth-first search:
# * selecting next variable to assign
# * predefined order (not so good)
# * MRV heuristic: variable with the minimum number of remaining values
# * degree heuristic: variable with largest number of constraints with other unassigned variables
#
#
# * selecting the next value to assign to the chosen variable
# * least-constraining value heuristic: value that rules out the fewest remaining values in other variables
#
#
# * propagate effect of an assignment, or inference
# * forward checking heuristic: remove values from other variables that break constraints with the assignment just made,
# * MAC heuristic: continue forward checking through other constraints affected by each new reduction in remaining values
#
#
# * more informed backtracking
# * chronological backtracking: the usual depth-first backtracking, most recent
# * backjumping: backtrack up further, to variable assignment that reduced the set of values available to the variable being assigned at the node where we fail
# ### Local Search
#
# Here is the procedure, from Figure 6.8, in python and pseudo-code:
#
#
# def min_conflicts(csp, max_steps):
# assignment = dictionary indexed by variables with values randomly assigned
# for i in range(max_steps):
# if assignment is a solution for csp:
# return assignment
# conflicted_variables = set of variables involved in broken constraints
# variable = one chosen randomly from conflicted_variables
# value = value for variable with minimum number of conflicts
# assignment[variable] = value
# return 'failure'
# ## Applications of Min-Conflicts
# ### Map Coloring Problem
#
# Let's try the map-coloring problem. What is the initial state? Must
# be a complete assignment. Let's just pick colors at random.
#
#
#
#
# Many ideas exist for guiding the depth-first search:
# * selecting next variable to assign
# * predefined order (not so good)
# * MRV heuristic: variable with the minimum number of remaining values
# * degree heuristic: variable with largest number of constraints with other unassigned variables
#
#
# * selecting the next value to assign to the chosen variable
# * least-constraining value heuristic: value that rules out the fewest remaining values in other variables
#
#
# * propagate effect of an assignment, or inference
# * forward checking heuristic: remove values from other variables that break constraints with the assignment just made,
# * MAC heuristic: continue forward checking through other constraints affected by each new reduction in remaining values
#
#
# * more informed backtracking
# * chronological backtracking: the usual depth-first backtracking, most recent
# * backjumping: backtrack up further, to variable assignment that reduced the set of values available to the variable being assigned at the node where we fail
# ### Local Search
#
# Here is the procedure, from Figure 6.8, in python and pseudo-code:
#
#
# def min_conflicts(csp, max_steps):
# assignment = dictionary indexed by variables with values randomly assigned
# for i in range(max_steps):
# if assignment is a solution for csp:
# return assignment
# conflicted_variables = set of variables involved in broken constraints
# variable = one chosen randomly from conflicted_variables
# value = value for variable with minimum number of conflicts
# assignment[variable] = value
# return 'failure'
# ## Applications of Min-Conflicts
# ### Map Coloring Problem
#
# Let's try the map-coloring problem. What is the initial state? Must
# be a complete assignment. Let's just pick colors at random.
#
#  #
# Now what are the one-step neighbors of this starting state? Local
# search for CSP proceeds by randomly picking a variable from ones with
# assigned values that break a constraint. The new value assigned to
# that variable is one that has a minimum of conflicts with other
# variable assignments in this state.
#
# Five variables have conflicts.
# Let's pick New South Wales, at random, among set of conflicted variables. Blue conflicts with two variables, red
# conflicts with none, and green conflicts with one. So, set color of New South Wales to red.
#
#
#
# Now what are the one-step neighbors of this starting state? Local
# search for CSP proceeds by randomly picking a variable from ones with
# assigned values that break a constraint. The new value assigned to
# that variable is one that has a minimum of conflicts with other
# variable assignments in this state.
#
# Five variables have conflicts.
# Let's pick New South Wales, at random, among set of conflicted variables. Blue conflicts with two variables, red
# conflicts with none, and green conflicts with one. So, set color of New South Wales to red.
#
#  #
# Now three variables have conflicts. Let's pick Victoria. For
# Victoria, green has no conflicts, red and blue each have one, so pick green.
#
#
#
# Now three variables have conflicts. Let's pick Victoria. For
# Victoria, green has no conflicts, red and blue each have one, so pick green.
#
#  #
# Now two variables have conflicts. Pick Northern Territory. For
# Northern Territory, red, green and blue each conflict with one.
# Pick green randomly.
#
#
#
# Now two variables have conflicts. Pick Northern Territory. For
# Northern Territory, red, green and blue each conflict with one.
# Pick green randomly.
#
#  #
# Again, only two variables have conflicts. Pick Queensland. For Queensland,
# red, green and blue each have one conflict. Pick red randomly.
#
#
# Again, only two variables have conflicts. Pick Queensland. For Queensland,
# red, green and blue each have one conflict. Pick red randomly.
#  #
# Again, two variables. Pick New South Wales. For New South Wales, green,
# red and blue
# conflict with one. Pick green randomly.
#
#
#
# Again, two variables. Pick New South Wales. For New South Wales, green,
# red and blue
# conflict with one. Pick green randomly.
#
#  #
# Again, two variables. Pick Victoria. For Victoria, red has no
# conflicts, blue and green have one. So pick red.
#
#
#
# Again, two variables. Pick Victoria. For Victoria, red has no
# conflicts, blue and green have one. So pick red.
#
#  #
# And, TA-DA, no conflicts remain. We have found a solution.
# ### N-Queens Problem Solved
#
# Place $n$ queens on a chess board such that no queen attacks another.
#
# In figure below, $h$ is the number of pairs of queens that attack each other. We want to find an arrangement of queens for which $h=0$.
#
#
#
# And, TA-DA, no conflicts remain. We have found a solution.
# ### N-Queens Problem Solved
#
# Place $n$ queens on a chess board such that no queen attacks another.
#
# In figure below, $h$ is the number of pairs of queens that attack each other. We want to find an arrangement of queens for which $h=0$.
#
# 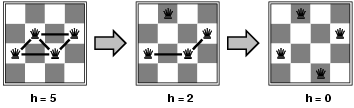 #
# Can solve 8-queens problem quickly, but for large $n$,$n$-queens problems take a very long time....right?
#
#
# Wrong! Even when $n=1,000,000$ solutions can be found in an average of 50 steps!
#
# Following figures are from Minton, et al.'s, paper linked below.
#
#
#
# Can solve 8-queens problem quickly, but for large $n$,$n$-queens problems take a very long time....right?
#
#
# Wrong! Even when $n=1,000,000$ solutions can be found in an average of 50 steps!
#
# Following figures are from Minton, et al.'s, paper linked below.
#
# 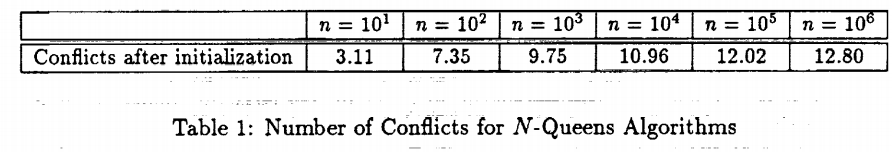 #
#
#
#  #
#
# Given a random initial state, min-conflicts can solve an n-queens problem in almost constant time for arbitrary $n$ with high probability (such as $n=10,000,000$).
#
# A similar statement seems to be true for any randomly-generated CSP except in a narrow range of the ratio $R$:
#
#
#
#
# Given a random initial state, min-conflicts can solve an n-queens problem in almost constant time for arbitrary $n$ with high probability (such as $n=10,000,000$).
#
# A similar statement seems to be true for any randomly-generated CSP except in a narrow range of the ratio $R$:
#
# 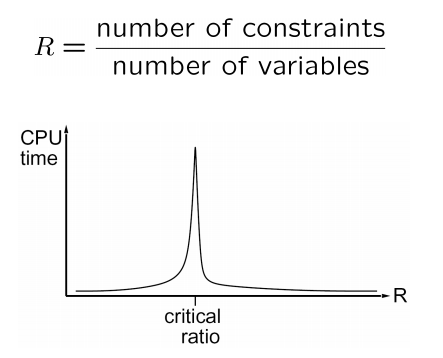 # ### Scheduling Experiments on Hubble Space Telescope
#
# Scheduling a week of tasks for the Hubble Space Telescope takes about 10
# minutes with local search. Previously it had taken three weeks.
#
#
# ### Scheduling Experiments on Hubble Space Telescope
#
# Scheduling a week of tasks for the Hubble Space Telescope takes about 10
# minutes with local search. Previously it had taken three weeks.
#
#  #
# from [this site](https://frontierfields.org/2014/06/23/how-hubble-observations-are-scheduled/). And check out Hubble's [amazing photos and videos](https://hubblesite.org/).
#
# [The min-conflicts heuristic: Experimental and theoretical results](https://www.researchgate.net/publication/24322715_The_min-conflicts_heuristic_Experimental_and_theoretical_results), by Steven Minton, Andrew Philips, Mark Johnston, and Philip Laird, September 1991.
# In[ ]:
#
# from [this site](https://frontierfields.org/2014/06/23/how-hubble-observations-are-scheduled/). And check out Hubble's [amazing photos and videos](https://hubblesite.org/).
#
# [The min-conflicts heuristic: Experimental and theoretical results](https://www.researchgate.net/publication/24322715_The_min-conflicts_heuristic_Experimental_and_theoretical_results), by Steven Minton, Andrew Philips, Mark Johnston, and Philip Laird, September 1991.
# In[ ]:
 #
# What are the variables? What are the domains of values for each
# variable?
#
# What are the constraints? No neighboring regions can have the same
# color. Can be expressed in a constraint graph with
# * nodes representing variables
# * edges representing pairwise (binary) constraints
#
#
#
# What are the variables? What are the domains of values for each
# variable?
#
# What are the constraints? No neighboring regions can have the same
# color. Can be expressed in a constraint graph with
# * nodes representing variables
# * edges representing pairwise (binary) constraints
#
#  #
# A popular constraint propagation algorithm is AC-3. "AC" is for
# "arc-consistency". 3 is for third version. It proceeds by removing
# values from the domains of variables at either end of an arc to
# maintain the constraints.
#
# A stronger version of this approach is called path-consistency (PC-2). It considers triplets of variables at a time.
#
# | | | WA | NT | SA | Q | NSW | V | T |
# | :--: | :--: | :--: | :--: | :--: | :--: | :--: | :--: | :--: |
# | 1 | | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | 2 | WA-NT considering SA | (r) | (g) | (b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (g) | (r) | (b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (g) | (r) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (r) | (g) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | 3 | NT-SA considering Q | (r) | (g) | (b) | (r) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (g) | (r) | (b) | (g) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (g) | (r) | (b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (r) | (g) | (b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | 4 | and so on ... |
# ### Backtracking Search
#
# Assign value to one variable at a time. Do depth-first search with backtracking.
#
#
#
# A popular constraint propagation algorithm is AC-3. "AC" is for
# "arc-consistency". 3 is for third version. It proceeds by removing
# values from the domains of variables at either end of an arc to
# maintain the constraints.
#
# A stronger version of this approach is called path-consistency (PC-2). It considers triplets of variables at a time.
#
# | | | WA | NT | SA | Q | NSW | V | T |
# | :--: | :--: | :--: | :--: | :--: | :--: | :--: | :--: | :--: |
# | 1 | | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | 2 | WA-NT considering SA | (r) | (g) | (b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (g) | (r) | (b) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (g) | (r) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (r) | (g) | (r,g,b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | 3 | NT-SA considering Q | (r) | (g) | (b) | (r) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (g) | (r) | (b) | (g) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (g) | (r) | (b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | | | (b) | (r) | (g) | (b) | (r,g,b) | (r,g,b) | (r,g,b) |
# | 4 | and so on ... |
# ### Backtracking Search
#
# Assign value to one variable at a time. Do depth-first search with backtracking.
#
#  #
#  #
#  #
#
# Many ideas exist for guiding the depth-first search:
# * selecting next variable to assign
# * predefined order (not so good)
# * MRV heuristic: variable with the minimum number of remaining values
# * degree heuristic: variable with largest number of constraints with other unassigned variables
#
#
# * selecting the next value to assign to the chosen variable
# * least-constraining value heuristic: value that rules out the fewest remaining values in other variables
#
#
# * propagate effect of an assignment, or inference
# * forward checking heuristic: remove values from other variables that break constraints with the assignment just made,
# * MAC heuristic: continue forward checking through other constraints affected by each new reduction in remaining values
#
#
# * more informed backtracking
# * chronological backtracking: the usual depth-first backtracking, most recent
# * backjumping: backtrack up further, to variable assignment that reduced the set of values available to the variable being assigned at the node where we fail
# ### Local Search
#
# Here is the procedure, from Figure 6.8, in python and pseudo-code:
#
#
# def min_conflicts(csp, max_steps):
# assignment = dictionary indexed by variables with values randomly assigned
# for i in range(max_steps):
# if assignment is a solution for csp:
# return assignment
# conflicted_variables = set of variables involved in broken constraints
# variable = one chosen randomly from conflicted_variables
# value = value for variable with minimum number of conflicts
# assignment[variable] = value
# return 'failure'
# ## Applications of Min-Conflicts
# ### Map Coloring Problem
#
# Let's try the map-coloring problem. What is the initial state? Must
# be a complete assignment. Let's just pick colors at random.
#
#
#
#
# Many ideas exist for guiding the depth-first search:
# * selecting next variable to assign
# * predefined order (not so good)
# * MRV heuristic: variable with the minimum number of remaining values
# * degree heuristic: variable with largest number of constraints with other unassigned variables
#
#
# * selecting the next value to assign to the chosen variable
# * least-constraining value heuristic: value that rules out the fewest remaining values in other variables
#
#
# * propagate effect of an assignment, or inference
# * forward checking heuristic: remove values from other variables that break constraints with the assignment just made,
# * MAC heuristic: continue forward checking through other constraints affected by each new reduction in remaining values
#
#
# * more informed backtracking
# * chronological backtracking: the usual depth-first backtracking, most recent
# * backjumping: backtrack up further, to variable assignment that reduced the set of values available to the variable being assigned at the node where we fail
# ### Local Search
#
# Here is the procedure, from Figure 6.8, in python and pseudo-code:
#
#
# def min_conflicts(csp, max_steps):
# assignment = dictionary indexed by variables with values randomly assigned
# for i in range(max_steps):
# if assignment is a solution for csp:
# return assignment
# conflicted_variables = set of variables involved in broken constraints
# variable = one chosen randomly from conflicted_variables
# value = value for variable with minimum number of conflicts
# assignment[variable] = value
# return 'failure'
# ## Applications of Min-Conflicts
# ### Map Coloring Problem
#
# Let's try the map-coloring problem. What is the initial state? Must
# be a complete assignment. Let's just pick colors at random.
#
#  #
# Now what are the one-step neighbors of this starting state? Local
# search for CSP proceeds by randomly picking a variable from ones with
# assigned values that break a constraint. The new value assigned to
# that variable is one that has a minimum of conflicts with other
# variable assignments in this state.
#
# Five variables have conflicts.
# Let's pick New South Wales, at random, among set of conflicted variables. Blue conflicts with two variables, red
# conflicts with none, and green conflicts with one. So, set color of New South Wales to red.
#
#
#
# Now what are the one-step neighbors of this starting state? Local
# search for CSP proceeds by randomly picking a variable from ones with
# assigned values that break a constraint. The new value assigned to
# that variable is one that has a minimum of conflicts with other
# variable assignments in this state.
#
# Five variables have conflicts.
# Let's pick New South Wales, at random, among set of conflicted variables. Blue conflicts with two variables, red
# conflicts with none, and green conflicts with one. So, set color of New South Wales to red.
#
#  #
# Now three variables have conflicts. Let's pick Victoria. For
# Victoria, green has no conflicts, red and blue each have one, so pick green.
#
#
#
# Now three variables have conflicts. Let's pick Victoria. For
# Victoria, green has no conflicts, red and blue each have one, so pick green.
#
#  #
# Now two variables have conflicts. Pick Northern Territory. For
# Northern Territory, red, green and blue each conflict with one.
# Pick green randomly.
#
#
#
# Now two variables have conflicts. Pick Northern Territory. For
# Northern Territory, red, green and blue each conflict with one.
# Pick green randomly.
#
#  #
# Again, only two variables have conflicts. Pick Queensland. For Queensland,
# red, green and blue each have one conflict. Pick red randomly.
#
#
# Again, only two variables have conflicts. Pick Queensland. For Queensland,
# red, green and blue each have one conflict. Pick red randomly.
#  #
# Again, two variables. Pick New South Wales. For New South Wales, green,
# red and blue
# conflict with one. Pick green randomly.
#
#
#
# Again, two variables. Pick New South Wales. For New South Wales, green,
# red and blue
# conflict with one. Pick green randomly.
#
#  #
# Again, two variables. Pick Victoria. For Victoria, red has no
# conflicts, blue and green have one. So pick red.
#
#
#
# Again, two variables. Pick Victoria. For Victoria, red has no
# conflicts, blue and green have one. So pick red.
#
#  #
# And, TA-DA, no conflicts remain. We have found a solution.
# ### N-Queens Problem Solved
#
# Place $n$ queens on a chess board such that no queen attacks another.
#
# In figure below, $h$ is the number of pairs of queens that attack each other. We want to find an arrangement of queens for which $h=0$.
#
#
#
# And, TA-DA, no conflicts remain. We have found a solution.
# ### N-Queens Problem Solved
#
# Place $n$ queens on a chess board such that no queen attacks another.
#
# In figure below, $h$ is the number of pairs of queens that attack each other. We want to find an arrangement of queens for which $h=0$.
#
#  #
# Can solve 8-queens problem quickly, but for large $n$,$n$-queens problems take a very long time....right?
#
#
# Wrong! Even when $n=1,000,000$ solutions can be found in an average of 50 steps!
#
# Following figures are from Minton, et al.'s, paper linked below.
#
#
#
# Can solve 8-queens problem quickly, but for large $n$,$n$-queens problems take a very long time....right?
#
#
# Wrong! Even when $n=1,000,000$ solutions can be found in an average of 50 steps!
#
# Following figures are from Minton, et al.'s, paper linked below.
#
# 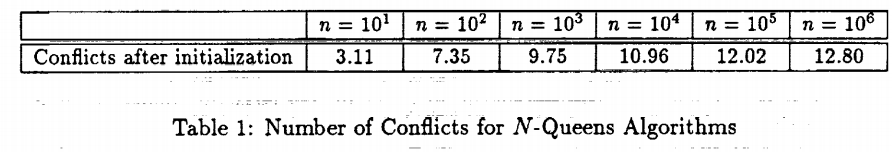 #
#
#
#  #
#
# Given a random initial state, min-conflicts can solve an n-queens problem in almost constant time for arbitrary $n$ with high probability (such as $n=10,000,000$).
#
# A similar statement seems to be true for any randomly-generated CSP except in a narrow range of the ratio $R$:
#
#
#
#
# Given a random initial state, min-conflicts can solve an n-queens problem in almost constant time for arbitrary $n$ with high probability (such as $n=10,000,000$).
#
# A similar statement seems to be true for any randomly-generated CSP except in a narrow range of the ratio $R$:
#
#  # ### Scheduling Experiments on Hubble Space Telescope
#
# Scheduling a week of tasks for the Hubble Space Telescope takes about 10
# minutes with local search. Previously it had taken three weeks.
#
#
# ### Scheduling Experiments on Hubble Space Telescope
#
# Scheduling a week of tasks for the Hubble Space Telescope takes about 10
# minutes with local search. Previously it had taken three weeks.
#
#  #
# from [this site](https://frontierfields.org/2014/06/23/how-hubble-observations-are-scheduled/). And check out Hubble's [amazing photos and videos](https://hubblesite.org/).
#
# [The min-conflicts heuristic: Experimental and theoretical results](https://www.researchgate.net/publication/24322715_The_min-conflicts_heuristic_Experimental_and_theoretical_results), by Steven Minton, Andrew Philips, Mark Johnston, and Philip Laird, September 1991.
# In[ ]:
#
# from [this site](https://frontierfields.org/2014/06/23/how-hubble-observations-are-scheduled/). And check out Hubble's [amazing photos and videos](https://hubblesite.org/).
#
# [The min-conflicts heuristic: Experimental and theoretical results](https://www.researchgate.net/publication/24322715_The_min-conflicts_heuristic_Experimental_and_theoretical_results), by Steven Minton, Andrew Philips, Mark Johnston, and Philip Laird, September 1991.
# In[ ]: