#!/usr/bin/env python
# coding: utf-8
# # Conjuntos con Python
# *Esta notebook fue creada originalmente como un blog post por [Raúl E. López Briega](http://relopezbriega.com.ar/) en [Mi blog sobre Python](http://relopezbriega.github.io). El contenido esta bajo la licencia BSD.*
# 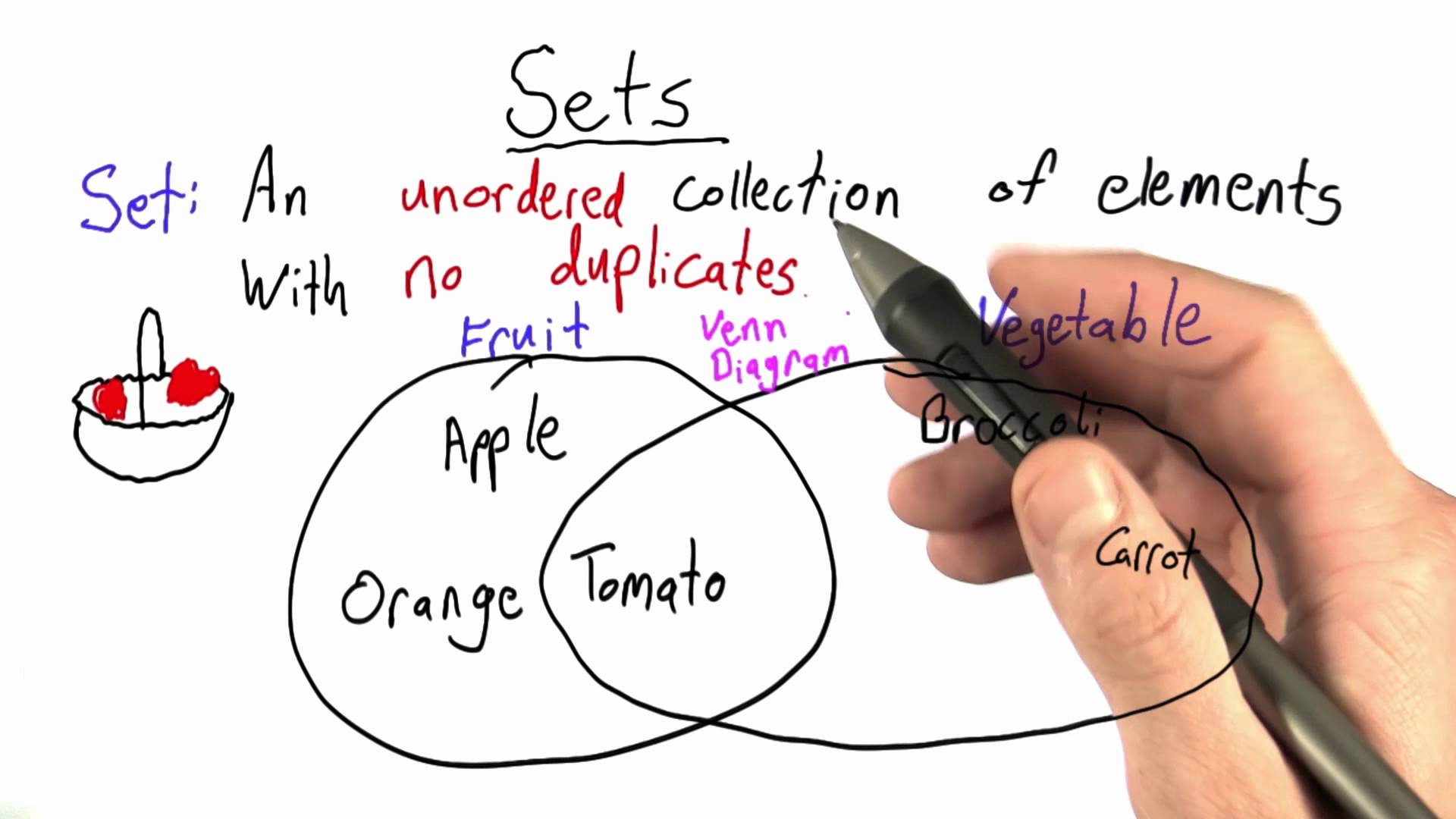 # ## Introducción
#
# Una característica notable de los seres humanos es su inherente necesidad y capacidad de agrupar objetos de acuerdo a criterios específicos.
# La idea de la clasificación de ciertos objetos en grupos similares, o *[conjuntos](https://es.wikipedia.org/wiki/Conjunto)*, es uno de los conceptos más fundamentales de la matemática moderna. La [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos) ha sido el marco unificador para todas las matemáticas desde que el matemático alemán [Georg Cantor](https://es.wikipedia.org/wiki/Georg_Cantor) la formulara alrededor de 1870. Ningún campo de las matemáticas podría describirse hoy en día sin hacer referencia a algún tipo de [conjunto](https://es.wikipedia.org/wiki/Conjunto) abstracto.
# En términos más generales, el concepto de *membresía* de un [conjunto](https://es.wikipedia.org/wiki/Conjunto), que se encuentra en el corazón de la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos), explica cómo sentencias con sustantivos y predicados son formulados en nuestro lenguaje, o en cualquier lenguaje abstracto como las matemáticas. Debido a esto, la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos) está íntimamente ligada a la [lógica](https://es.wikipedia.org/wiki/L%C3%B3gica) y sirve de base para todas las matemáticas.
#
# ## ¿Qué es un conjunto?
#
# **Un [conjunto](https://es.wikipedia.org/wiki/Conjunto) es una colección de objetos distintos, a menudo llamados elementos o miembros**. Existen dos características hacen de los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) algo totalmente distinto a cualquier otra colección de objetos. En primer lugar, un [conjunto](https://es.wikipedia.org/wiki/Conjunto) está siempre "bien definido", es decir que si realizamos la pregunta *¿Este objeto particular, se encuentra en esta colección?*; siempre debe existir una respuesta clara por sí o por no basada en una regla o algunos criterios dados. La segunda característica, es que no hay dos miembros de
# un mismo [conjunto](https://es.wikipedia.org/wiki/Conjunto) que sean exactamente iguales, es decir, que no hay elementos repetidos.
# Un [conjunto](https://es.wikipedia.org/wiki/Conjunto) puede contener cualquier cosa imaginable, incluyendo números, letras, colores, incluso otros [conjuntos](https://es.wikipedia.org/wiki/Conjunto)!. Sin embargo, ninguno de los objetos del [conjunto](https://es.wikipedia.org/wiki/Conjunto) puede ser el propio [conjunto](https://es.wikipedia.org/wiki/Conjunto). Descartamos esta posibilidad para evitar encontrarnos con la [Paradoja de Russell](https://es.wikipedia.org/wiki/Paradoja_de_Russell), un problema famoso en la lógica matemática desenterrado por el gran lógico británico [Bertrand Russell](https://es.wikipedia.org/wiki/Bertrand_Russell) en 1901.
#
# ## Notación de Conjuntos
#
# Cuando escribimos a los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) utilizamos letras mayúsculas para sus nombres y para representar al [conjunto](https://es.wikipedia.org/wiki/Conjunto) propiamente dicho simplemente listamos sus elementos separándolos por comas y luego englobamos todos estos elementos dentro de un par de llaves. Así, por ejemplo, A = {1,2,3, ..., 10} es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de los 10 primeros [números naturales](https://es.wikipedia.org/wiki/N%C3%BAmero_natural) o para *contar*, B = {Rojo, Azul, Verde} es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de colores primarios, N = {1,2,3, ...} es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de todos los [números naturales](https://es.wikipedia.org/wiki/N%C3%BAmero_natural), y Z = {..., - 3, -2, -1,0,1,2,3, ...}
# es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de todos los [números enteros](https://es.wikipedia.org/wiki/N%C3%BAmero_entero). Los puntos suspensivos "..." se utilizan para describir el carácter *infinito* de los números en los conjuntos N y Z.
#
# También se utiliza el símbolo $ \in $ para expresar que determina objeto pertenece o es *miembro* de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) y el símbolo $ \notin $ para indicar que no pertenece a un [conjunto](https://es.wikipedia.org/wiki/Conjunto). Utilizando los ejemplos anteriores, podríamos por ejemplo escribir que $7 \in A$ y $12 \notin A$.
#
# Dado que muchos [conjuntos](https://es.wikipedia.org/wiki/Conjunto) no se pueden describir listando todos sus miembros, ya que en muchos casos esto es imposible, también se utiliza la mucho más potente notación de constructor de conjuntos o predicado. En esta notación escribimos el conjunto de acuerdo a qué tipos de objetos pertenecen al [conjunto](https://es.wikipedia.org/wiki/Conjunto), que se colocan a la izquierda del símbolo "|", que significa "de tal manera que," dentro de las llaves; así como las condiciones que estos objetos deben cumplir para pertenecer al [conjunto](https://es.wikipedia.org/wiki/Conjunto), las cuales se colocan a la derecha de "|" dentro de las llaves. Por ejemplo, el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de los [números racionales](https://es.wikipedia.org/wiki/N%C3%BAmero_racional), o fracciones, que se denota por Q no puede ser descrito por el método de listar todos sus miembros. En su lugar, se define a Q utilizando la notación de predicado de la siguiente manera:
# $Q=\{\frac{p}{q} \mid p, q \in Z$ y $q \ne 0 \}$
# Esto se lee "Q es el conjunto de todas las fracciones de la forma p sobre q, tal que p y q son números enteros y q no es cero." También podríamos escribir al conjunto A de nuestro ejemplo anterior como $A = \{x \mid x \in N$ y
# $x < 11\}$.
#
# ## Conjuntos numéricos
#
# Dentro de las matemáticas, los principales [conjuntos](https://es.wikipedia.org/wiki/Conjunto) numéricos que podemos encontrar y que tienen un carácter universal son:
#
# * $\mathbb{N} = \{1,2,3, ...\}$ es el conjunto de los [números naturales](https://es.wikipedia.org/wiki/N%C3%BAmero_natural).
# * $\mathbb{W} = \{0,1,2,3, ...\}$ es el conjunto de los [números enteros](https://es.wikipedia.org/wiki/N%C3%BAmero_entero) positivos.
# * $\mathbb{Z} = \{...,-3,-2,-1,0,1,2,3, ...\}$ es el conjunto de todos los [números enteros](https://es.wikipedia.org/wiki/N%C3%BAmero_entero).
# * $\mathbb{Q} =\{\frac{p}{q} \mid p, q \in Z$ y $q \ne 0 \}$ es el conjunto de los [números racionales](https://es.wikipedia.org/wiki/N%C3%BAmero_racional).
# * $\mathbb{R}$, es el conjunto de los [números reales](https://es.wikipedia.org/wiki/N%C3%BAmero_real). Estos son todos los números que pueden ser colocados en una recta numérica unidimensional que se extiende sin fin tanto en negativo como positivo.
# * $\mathbb{I}$, es el conjunto de los [números irracionales](https://es.wikipedia.org/wiki/N%C3%BAmero_irracional). Algunos de los números más importantes en matemáticas pertenecen a este conjunto,incluyendo $\pi, \sqrt{2}, e$ y $\phi$.
# * $\mathbb{C}$, es el conjunto de los [números complejos](https://es.wikipedia.org/wiki/N%C3%BAmero_complejo). Estos son los números que contienen una parte real y otra parte imaginaria.
#
# ## Igualdad entre conjuntos
#
# El concepto de igualdad en los [conjuntos](https://es.wikipedia.org/wiki/Conjunto), difiere levemente del clásico concepto de igualdad que solemos tener. Dos conjuntos A y B se dice que son iguales (expresado por A = B), si y sólo si ambos [conjuntos](https://es.wikipedia.org/wiki/Conjunto) tienen exactamente los mismos elementos. Por ejemplo el [conjunto](https://es.wikipedia.org/wiki/Conjunto) A={1,2,3,4} es igual al [conjunto](https://es.wikipedia.org/wiki/Conjunto) B={4,3,2,1}.
# Un [conjunto](https://es.wikipedia.org/wiki/Conjunto) importante, y que todavía no hemos mencionado es el **[conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo)**, el cual no tiene elementos y por tanto no puede ser igualado con ningún otro [conjunto](https://es.wikipedia.org/wiki/Conjunto). Se expresa con el símbolo $\emptyset$ o {}.
#
# ## Cardinalidad
#
# La [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A es el número de elementos que pertenecen a A y lo expresamos como n(A). La [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) puede ser pensada tambien como una medida de su "tamaño". Si la [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) es un [número entero](https://es.wikipedia.org/wiki/N%C3%BAmero_entero), entonces el conjunto se dice que es finito. De lo contrario, el conjunto se dice que es infinito. Así por ejemplo la [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) del [conjunto](https://es.wikipedia.org/wiki/Conjunto) A={1,2,...,9,10} es 10 y lo expresamos como n(A)=10.
#
# ## Subconjunto y subconjunto propio
#
# Si todos los elementos de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A son también elementos de otro [conjunto](https://es.wikipedia.org/wiki/Conjunto) B, entonces A se llama un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) de B y lo expresamos como $A \subseteq B$. En cierto sentido, se puede
# pensar al [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) A como dentro, o contenido en el [conjunto](https://es.wikipedia.org/wiki/Conjunto) B.
# Si un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A es un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) de B y los dos [conjuntos](https://es.wikipedia.org/wiki/Conjunto) no son iguales, entonces llamamos A un [subconjunto propio](https://es.wikipedia.org/wiki/Subconjunto#Subconjunto_propio) de B y lo expresamos como $A \subset B$. En este caso, se dice que el [conjunto](https://es.wikipedia.org/wiki/Conjunto) A esta propiamente contenido en B.
# Algunas propiedades importantes relacionadas con [subconjuntos](https://es.wikipedia.org/wiki/Subconjunto) y [subconjuntos propios](https://es.wikipedia.org/wiki/Subconjunto#Subconjunto_propio) son las siguientes:
#
# * Cualquier [conjunto](https://es.wikipedia.org/wiki/Conjunto) A es un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) de sí mismo. Por lo tanto $A \subseteq A$. Esto es claramente cierto.
# * Menos obvio es el hecho de que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) es un subconjunto de cualquier conjunto A. Por lo tanto $\emptyset \subseteq A$. Esta propiedad se prueba a través de la contradicción, ya que si asumimos que existe un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A del que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) no es un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto), entonces esto quiere decir que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) debe contener un elemento que no se encuentra en A y esto es absurdo ya que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) no contiene ningún elemento.
# * El [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) es un [subconjunto propio](https://es.wikipedia.org/wiki/Subconjunto#Subconjunto_propio) de cualquier [conjunto](https://es.wikipedia.org/wiki/Conjunto) A, siempre y cuando A no se también un [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo).
# * Para los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) finitos A y B, si $A \subseteq B$, entonces $n(A) \leq n(B)$.
# * De forma similar, para los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) finitos A y B, si $A \subset B$, entonces $n(A) < n(B)$.
#
#
# ## Conjunto potencia
#
# El [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A, expresado por $P_{A}$, es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) formado por todos los distintos [subconjuntos](https://es.wikipedia.org/wiki/Subconjunto) de A. Así por ejemplo el [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) del [conjunto](https://es.wikipedia.org/wiki/Conjunto) $A=\{1,2,3\}$; va a ser igual a $P_{A}=\{\emptyset,\{1\},\{2\},\{3\},\{1,2\},\{2,3\}, \{1,3\},\{1,2,3\}\}$.
#
# Un teorema importante de la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos) establece que si A es un [conjunto](https://es.wikipedia.org/wiki/Conjunto) con k elementos, es decir que n(A) = k; entonces el [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) de A tiene exactamente $2^k$ elementos. Escribimos esto como $n(P_{A}) = 2^k$. En nuestro ejemplo anterior podemos ver que n(A)=3, por lo tanto $n(P_{A}) = 2^3$, lo que es igual a los 8 elementos que vimos que tiene el [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) de A.
#
# ## Algebra de conjuntos
#
# El [álgebra de conjuntos](https://es.wikipedia.org/wiki/%C3%81lgebra_de_conjuntos) es el estudio de las operaciones básicas que podemos realizar con los [conjuntos](https://es.wikipedia.org/wiki/Conjunto). Las operaciones básicas del álgebra de conjuntos son:
#
# * **Unión**. La [unión](https://es.wikipedia.org/wiki/Uni%C3%B3n_de_conjuntos) de dos conjuntos A y B es el conjunto $A \cup B$ que contiene todos los elementos de A y de B.
#
# ## Introducción
#
# Una característica notable de los seres humanos es su inherente necesidad y capacidad de agrupar objetos de acuerdo a criterios específicos.
# La idea de la clasificación de ciertos objetos en grupos similares, o *[conjuntos](https://es.wikipedia.org/wiki/Conjunto)*, es uno de los conceptos más fundamentales de la matemática moderna. La [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos) ha sido el marco unificador para todas las matemáticas desde que el matemático alemán [Georg Cantor](https://es.wikipedia.org/wiki/Georg_Cantor) la formulara alrededor de 1870. Ningún campo de las matemáticas podría describirse hoy en día sin hacer referencia a algún tipo de [conjunto](https://es.wikipedia.org/wiki/Conjunto) abstracto.
# En términos más generales, el concepto de *membresía* de un [conjunto](https://es.wikipedia.org/wiki/Conjunto), que se encuentra en el corazón de la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos), explica cómo sentencias con sustantivos y predicados son formulados en nuestro lenguaje, o en cualquier lenguaje abstracto como las matemáticas. Debido a esto, la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos) está íntimamente ligada a la [lógica](https://es.wikipedia.org/wiki/L%C3%B3gica) y sirve de base para todas las matemáticas.
#
# ## ¿Qué es un conjunto?
#
# **Un [conjunto](https://es.wikipedia.org/wiki/Conjunto) es una colección de objetos distintos, a menudo llamados elementos o miembros**. Existen dos características hacen de los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) algo totalmente distinto a cualquier otra colección de objetos. En primer lugar, un [conjunto](https://es.wikipedia.org/wiki/Conjunto) está siempre "bien definido", es decir que si realizamos la pregunta *¿Este objeto particular, se encuentra en esta colección?*; siempre debe existir una respuesta clara por sí o por no basada en una regla o algunos criterios dados. La segunda característica, es que no hay dos miembros de
# un mismo [conjunto](https://es.wikipedia.org/wiki/Conjunto) que sean exactamente iguales, es decir, que no hay elementos repetidos.
# Un [conjunto](https://es.wikipedia.org/wiki/Conjunto) puede contener cualquier cosa imaginable, incluyendo números, letras, colores, incluso otros [conjuntos](https://es.wikipedia.org/wiki/Conjunto)!. Sin embargo, ninguno de los objetos del [conjunto](https://es.wikipedia.org/wiki/Conjunto) puede ser el propio [conjunto](https://es.wikipedia.org/wiki/Conjunto). Descartamos esta posibilidad para evitar encontrarnos con la [Paradoja de Russell](https://es.wikipedia.org/wiki/Paradoja_de_Russell), un problema famoso en la lógica matemática desenterrado por el gran lógico británico [Bertrand Russell](https://es.wikipedia.org/wiki/Bertrand_Russell) en 1901.
#
# ## Notación de Conjuntos
#
# Cuando escribimos a los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) utilizamos letras mayúsculas para sus nombres y para representar al [conjunto](https://es.wikipedia.org/wiki/Conjunto) propiamente dicho simplemente listamos sus elementos separándolos por comas y luego englobamos todos estos elementos dentro de un par de llaves. Así, por ejemplo, A = {1,2,3, ..., 10} es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de los 10 primeros [números naturales](https://es.wikipedia.org/wiki/N%C3%BAmero_natural) o para *contar*, B = {Rojo, Azul, Verde} es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de colores primarios, N = {1,2,3, ...} es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de todos los [números naturales](https://es.wikipedia.org/wiki/N%C3%BAmero_natural), y Z = {..., - 3, -2, -1,0,1,2,3, ...}
# es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de todos los [números enteros](https://es.wikipedia.org/wiki/N%C3%BAmero_entero). Los puntos suspensivos "..." se utilizan para describir el carácter *infinito* de los números en los conjuntos N y Z.
#
# También se utiliza el símbolo $ \in $ para expresar que determina objeto pertenece o es *miembro* de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) y el símbolo $ \notin $ para indicar que no pertenece a un [conjunto](https://es.wikipedia.org/wiki/Conjunto). Utilizando los ejemplos anteriores, podríamos por ejemplo escribir que $7 \in A$ y $12 \notin A$.
#
# Dado que muchos [conjuntos](https://es.wikipedia.org/wiki/Conjunto) no se pueden describir listando todos sus miembros, ya que en muchos casos esto es imposible, también se utiliza la mucho más potente notación de constructor de conjuntos o predicado. En esta notación escribimos el conjunto de acuerdo a qué tipos de objetos pertenecen al [conjunto](https://es.wikipedia.org/wiki/Conjunto), que se colocan a la izquierda del símbolo "|", que significa "de tal manera que," dentro de las llaves; así como las condiciones que estos objetos deben cumplir para pertenecer al [conjunto](https://es.wikipedia.org/wiki/Conjunto), las cuales se colocan a la derecha de "|" dentro de las llaves. Por ejemplo, el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de los [números racionales](https://es.wikipedia.org/wiki/N%C3%BAmero_racional), o fracciones, que se denota por Q no puede ser descrito por el método de listar todos sus miembros. En su lugar, se define a Q utilizando la notación de predicado de la siguiente manera:
# $Q=\{\frac{p}{q} \mid p, q \in Z$ y $q \ne 0 \}$
# Esto se lee "Q es el conjunto de todas las fracciones de la forma p sobre q, tal que p y q son números enteros y q no es cero." También podríamos escribir al conjunto A de nuestro ejemplo anterior como $A = \{x \mid x \in N$ y
# $x < 11\}$.
#
# ## Conjuntos numéricos
#
# Dentro de las matemáticas, los principales [conjuntos](https://es.wikipedia.org/wiki/Conjunto) numéricos que podemos encontrar y que tienen un carácter universal son:
#
# * $\mathbb{N} = \{1,2,3, ...\}$ es el conjunto de los [números naturales](https://es.wikipedia.org/wiki/N%C3%BAmero_natural).
# * $\mathbb{W} = \{0,1,2,3, ...\}$ es el conjunto de los [números enteros](https://es.wikipedia.org/wiki/N%C3%BAmero_entero) positivos.
# * $\mathbb{Z} = \{...,-3,-2,-1,0,1,2,3, ...\}$ es el conjunto de todos los [números enteros](https://es.wikipedia.org/wiki/N%C3%BAmero_entero).
# * $\mathbb{Q} =\{\frac{p}{q} \mid p, q \in Z$ y $q \ne 0 \}$ es el conjunto de los [números racionales](https://es.wikipedia.org/wiki/N%C3%BAmero_racional).
# * $\mathbb{R}$, es el conjunto de los [números reales](https://es.wikipedia.org/wiki/N%C3%BAmero_real). Estos son todos los números que pueden ser colocados en una recta numérica unidimensional que se extiende sin fin tanto en negativo como positivo.
# * $\mathbb{I}$, es el conjunto de los [números irracionales](https://es.wikipedia.org/wiki/N%C3%BAmero_irracional). Algunos de los números más importantes en matemáticas pertenecen a este conjunto,incluyendo $\pi, \sqrt{2}, e$ y $\phi$.
# * $\mathbb{C}$, es el conjunto de los [números complejos](https://es.wikipedia.org/wiki/N%C3%BAmero_complejo). Estos son los números que contienen una parte real y otra parte imaginaria.
#
# ## Igualdad entre conjuntos
#
# El concepto de igualdad en los [conjuntos](https://es.wikipedia.org/wiki/Conjunto), difiere levemente del clásico concepto de igualdad que solemos tener. Dos conjuntos A y B se dice que son iguales (expresado por A = B), si y sólo si ambos [conjuntos](https://es.wikipedia.org/wiki/Conjunto) tienen exactamente los mismos elementos. Por ejemplo el [conjunto](https://es.wikipedia.org/wiki/Conjunto) A={1,2,3,4} es igual al [conjunto](https://es.wikipedia.org/wiki/Conjunto) B={4,3,2,1}.
# Un [conjunto](https://es.wikipedia.org/wiki/Conjunto) importante, y que todavía no hemos mencionado es el **[conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo)**, el cual no tiene elementos y por tanto no puede ser igualado con ningún otro [conjunto](https://es.wikipedia.org/wiki/Conjunto). Se expresa con el símbolo $\emptyset$ o {}.
#
# ## Cardinalidad
#
# La [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A es el número de elementos que pertenecen a A y lo expresamos como n(A). La [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) puede ser pensada tambien como una medida de su "tamaño". Si la [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) es un [número entero](https://es.wikipedia.org/wiki/N%C3%BAmero_entero), entonces el conjunto se dice que es finito. De lo contrario, el conjunto se dice que es infinito. Así por ejemplo la [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) del [conjunto](https://es.wikipedia.org/wiki/Conjunto) A={1,2,...,9,10} es 10 y lo expresamos como n(A)=10.
#
# ## Subconjunto y subconjunto propio
#
# Si todos los elementos de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A son también elementos de otro [conjunto](https://es.wikipedia.org/wiki/Conjunto) B, entonces A se llama un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) de B y lo expresamos como $A \subseteq B$. En cierto sentido, se puede
# pensar al [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) A como dentro, o contenido en el [conjunto](https://es.wikipedia.org/wiki/Conjunto) B.
# Si un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A es un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) de B y los dos [conjuntos](https://es.wikipedia.org/wiki/Conjunto) no son iguales, entonces llamamos A un [subconjunto propio](https://es.wikipedia.org/wiki/Subconjunto#Subconjunto_propio) de B y lo expresamos como $A \subset B$. En este caso, se dice que el [conjunto](https://es.wikipedia.org/wiki/Conjunto) A esta propiamente contenido en B.
# Algunas propiedades importantes relacionadas con [subconjuntos](https://es.wikipedia.org/wiki/Subconjunto) y [subconjuntos propios](https://es.wikipedia.org/wiki/Subconjunto#Subconjunto_propio) son las siguientes:
#
# * Cualquier [conjunto](https://es.wikipedia.org/wiki/Conjunto) A es un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) de sí mismo. Por lo tanto $A \subseteq A$. Esto es claramente cierto.
# * Menos obvio es el hecho de que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) es un subconjunto de cualquier conjunto A. Por lo tanto $\emptyset \subseteq A$. Esta propiedad se prueba a través de la contradicción, ya que si asumimos que existe un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A del que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) no es un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto), entonces esto quiere decir que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) debe contener un elemento que no se encuentra en A y esto es absurdo ya que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) no contiene ningún elemento.
# * El [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) es un [subconjunto propio](https://es.wikipedia.org/wiki/Subconjunto#Subconjunto_propio) de cualquier [conjunto](https://es.wikipedia.org/wiki/Conjunto) A, siempre y cuando A no se también un [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo).
# * Para los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) finitos A y B, si $A \subseteq B$, entonces $n(A) \leq n(B)$.
# * De forma similar, para los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) finitos A y B, si $A \subset B$, entonces $n(A) < n(B)$.
#
#
# ## Conjunto potencia
#
# El [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A, expresado por $P_{A}$, es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) formado por todos los distintos [subconjuntos](https://es.wikipedia.org/wiki/Subconjunto) de A. Así por ejemplo el [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) del [conjunto](https://es.wikipedia.org/wiki/Conjunto) $A=\{1,2,3\}$; va a ser igual a $P_{A}=\{\emptyset,\{1\},\{2\},\{3\},\{1,2\},\{2,3\}, \{1,3\},\{1,2,3\}\}$.
#
# Un teorema importante de la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos) establece que si A es un [conjunto](https://es.wikipedia.org/wiki/Conjunto) con k elementos, es decir que n(A) = k; entonces el [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) de A tiene exactamente $2^k$ elementos. Escribimos esto como $n(P_{A}) = 2^k$. En nuestro ejemplo anterior podemos ver que n(A)=3, por lo tanto $n(P_{A}) = 2^3$, lo que es igual a los 8 elementos que vimos que tiene el [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) de A.
#
# ## Algebra de conjuntos
#
# El [álgebra de conjuntos](https://es.wikipedia.org/wiki/%C3%81lgebra_de_conjuntos) es el estudio de las operaciones básicas que podemos realizar con los [conjuntos](https://es.wikipedia.org/wiki/Conjunto). Las operaciones básicas del álgebra de conjuntos son:
#
# * **Unión**. La [unión](https://es.wikipedia.org/wiki/Uni%C3%B3n_de_conjuntos) de dos conjuntos A y B es el conjunto $A \cup B$ que contiene todos los elementos de A y de B.
#  #
# * **Intersección**. La [intersección](https://es.wikipedia.org/wiki/Intersecci%C3%B3n_de_conjuntos) de dos conjuntos A y B es el conjunto $A \cap B$ que contiene todos los elementos comunes de A y B.
#
#
# * **Intersección**. La [intersección](https://es.wikipedia.org/wiki/Intersecci%C3%B3n_de_conjuntos) de dos conjuntos A y B es el conjunto $A \cap B$ que contiene todos los elementos comunes de A y B.
#  #
# * **Diferencia**. La [diferencia](https://es.wikipedia.org/wiki/Diferencia_de_conjuntos) entre dos conjuntos A y B es el conjunto $A \setminus B$ que contiene todos los elementos de A que no pertenecen a B.
#
#
# * **Diferencia**. La [diferencia](https://es.wikipedia.org/wiki/Diferencia_de_conjuntos) entre dos conjuntos A y B es el conjunto $A \setminus B$ que contiene todos los elementos de A que no pertenecen a B.
#  #
# * **Complemento**. El [complemento](https://es.wikipedia.org/wiki/Complemento_de_un_conjunto) de un conjunto A es el conjunto $A^∁$ que contiene todos los elementos que no pertenecen a A.
#
#
# * **Complemento**. El [complemento](https://es.wikipedia.org/wiki/Complemento_de_un_conjunto) de un conjunto A es el conjunto $A^∁$ que contiene todos los elementos que no pertenecen a A.
#  #
# * **Producto cartesiano**. El [producto cartesiano](https://es.wikipedia.org/wiki/Producto_cartesiano) de dos conjuntos A y B es el conjunto $A \times B$ que contiene todos los pares ordenados (a, b) cuyo primer elemento pertenece a A y su segundo elemento pertenece a B.
#
#
# ## Conjuntos con Python
#
# Luego de todo este repaso por los fundamentos de la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos), es tiempo de ver como podemos utilizar a los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) dentro de [Python](https://www.python.org/); ya que el lenguaje trae como una de sus [estructuras de datos](https://es.wikipedia.org/wiki/Estructura_de_datos) por defecto a los [conjuntos](https://es.wikipedia.org/wiki/Conjunto). También veremos que podemos utilizar el *constructor* `FiniteSet` que nos proporciona [sympy](http://www.sympy.org/es/), el cual tiene ciertas ventajas sobre la versión por defecto de [Python](https://www.python.org/).
# In[1]:
# Creando un conjunto en python
A = {1,2,3}
A
# In[2]:
# Creando un conjunto a partir de una lista
lista = ["bananas", "manzanas", "naranjas", "limones"]
B = set(lista)
B
# In[3]:
# Los conjuntos eliminan los elementos duplicados
lista = ["bananas", "manzanas", "naranjas", "limones",
"bananas", "bananas", "limones", "naranjas"]
B = set(lista)
B
# In[4]:
# Creando el conjunto vacío
O = set()
O
# In[5]:
# Cardinalidad de un conjunto con len().
print("La cardinalidad del conjunto A = {0} es {1}".format(A,len(A)))
# In[6]:
# comprobando membresía
2 in A
# In[7]:
# Igualdad entre conjuntos. El orden de los elementos no importa.
A = {1,2,3,4}
B = {4,2,3,1}
A == B
# In[8]:
# Subconjunto. No hay distincion entre subconjunto y propio
# para el conjunto por defecto de python.
A = {1,2,3}
B = {1,2,3,4,5}
A.issubset(B)
# In[9]:
# Subconjunto propio
A.issubset(B) and A != B
# In[10]:
# Union de conjuntos
A = {1,2,3,4,5}
B = {4,5,6,7,8,9,10}
A.union(B)
# In[11]:
# Intersección de conjuntos
A.intersection(B)
# In[12]:
# Diferencia entre conjuntos
A - B
# In[13]:
B - A
# In[14]:
# Utilizando FiniteSet de sympy
from sympy import FiniteSet
C = FiniteSet(1, 2, 3)
C
# In[15]:
# Generando el conjunto potencia. Esto no se puede
# hacer utilizando el conjunto por defecto de python.
C.powerset()
# In[16]:
# Cardinalidad
print("La cardinalidad del conjunto potencia del conjunto C = {0} es {1}".
format(C, len(C.powerset())))
# In[17]:
# Igualdad
A = FiniteSet(1, 2, 3)
B = FiniteSet(1, 3, 2)
A == B
# In[18]:
A = FiniteSet(1, 2, 3)
B = FiniteSet(1, 3, 4)
A == B
# In[19]:
# Subconjunto y subconjunto propio
A = FiniteSet(1,2,3)
B = FiniteSet(1,2,3,4,5)
A.is_subset(B)
# In[20]:
A.is_proper_subset(B)
# In[21]:
# A == B. El test de subconjunto propio da falso
B = FiniteSet(2,1,3)
A.is_proper_subset(B)
# In[22]:
# Union de dos conjuntos
A = FiniteSet(1, 2, 3)
B = FiniteSet(2, 4, 6)
A.union(B)
# In[23]:
# Interseccion de dos conjuntos
A = FiniteSet(1, 2)
B = FiniteSet(2, 3)
A.intersect(B)
# In[24]:
# Diferencia entre conjuntos
A - B
# In[25]:
# Calculando el producto cartesiano. Con el conjunto por
# defecto de python no podemos hacer esto con el operador *
A = FiniteSet(1, 2)
B = FiniteSet(3, 4)
P = A * B
P
# In[26]:
for elem in P:
print(elem)
# In[27]:
# Elevar a la n potencia un conjunto. Calcula el n
# producto cartesiano del mismo conjunto.
A = FiniteSet(1, 2, 3, 4)
P2 = A ** 2
P2
# In[28]:
P3 = A ** 3
P3
# In[29]:
for elem in P3:
print(elem)
# In[30]:
# graficos embebidos
get_ipython().run_line_magic('matplotlib', 'inline')
# In[31]:
# Dibujanto el diagrama de venn de 2 conjuntos
from matplotlib_venn import venn2, venn2_circles
import matplotlib.pyplot as plt
A = FiniteSet(1, 3, 5, 7, 9, 11, 13, 15, 17, 19)
B = FiniteSet(2, 3, 5, 7, 11, 13, 17, 19, 8)
plt.figure(figsize=(6, 8))
v = venn2(subsets=[A, B], set_labels=('A', 'B'))
v.get_label_by_id('10').set_text(A - B)
v.get_label_by_id('11').set_text(A.intersection(B))
v.get_label_by_id('01').set_text(B - A)
c = venn2_circles(subsets=[A, B], linestyle='dashed')
c[0].set_ls('solid')
plt.show()
# Además de las aplicaciones que pueden tener los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) de [Python](https://www.python.org/) en matemáticas, los mismos también pueden ser una [estructura de datos](https://es.wikipedia.org/wiki/Estructura_de_datos) poderosa y ayudarnos a resolver varios problemas de programación en forma muy sencilla. A tenerlos en cuenta!
#
# Con esto termino este artículo; espero que les haya gustado y les sea de utilidad.
# Saludos!
#
# *Este post fue escrito utilizando IPython notebook. Pueden descargar este [notebook](https://github.com/relopezbriega/relopezbriega.github.io/blob/master/downloads/pythonSets.ipynb) o ver su version estática en [nbviewer](http://nbviewer.ipython.org/github/relopezbriega/relopezbriega.github.io/blob/master/downloads/pythonSets.ipynb).*
#
# * **Producto cartesiano**. El [producto cartesiano](https://es.wikipedia.org/wiki/Producto_cartesiano) de dos conjuntos A y B es el conjunto $A \times B$ que contiene todos los pares ordenados (a, b) cuyo primer elemento pertenece a A y su segundo elemento pertenece a B.
#
#
# ## Conjuntos con Python
#
# Luego de todo este repaso por los fundamentos de la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos), es tiempo de ver como podemos utilizar a los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) dentro de [Python](https://www.python.org/); ya que el lenguaje trae como una de sus [estructuras de datos](https://es.wikipedia.org/wiki/Estructura_de_datos) por defecto a los [conjuntos](https://es.wikipedia.org/wiki/Conjunto). También veremos que podemos utilizar el *constructor* `FiniteSet` que nos proporciona [sympy](http://www.sympy.org/es/), el cual tiene ciertas ventajas sobre la versión por defecto de [Python](https://www.python.org/).
# In[1]:
# Creando un conjunto en python
A = {1,2,3}
A
# In[2]:
# Creando un conjunto a partir de una lista
lista = ["bananas", "manzanas", "naranjas", "limones"]
B = set(lista)
B
# In[3]:
# Los conjuntos eliminan los elementos duplicados
lista = ["bananas", "manzanas", "naranjas", "limones",
"bananas", "bananas", "limones", "naranjas"]
B = set(lista)
B
# In[4]:
# Creando el conjunto vacío
O = set()
O
# In[5]:
# Cardinalidad de un conjunto con len().
print("La cardinalidad del conjunto A = {0} es {1}".format(A,len(A)))
# In[6]:
# comprobando membresía
2 in A
# In[7]:
# Igualdad entre conjuntos. El orden de los elementos no importa.
A = {1,2,3,4}
B = {4,2,3,1}
A == B
# In[8]:
# Subconjunto. No hay distincion entre subconjunto y propio
# para el conjunto por defecto de python.
A = {1,2,3}
B = {1,2,3,4,5}
A.issubset(B)
# In[9]:
# Subconjunto propio
A.issubset(B) and A != B
# In[10]:
# Union de conjuntos
A = {1,2,3,4,5}
B = {4,5,6,7,8,9,10}
A.union(B)
# In[11]:
# Intersección de conjuntos
A.intersection(B)
# In[12]:
# Diferencia entre conjuntos
A - B
# In[13]:
B - A
# In[14]:
# Utilizando FiniteSet de sympy
from sympy import FiniteSet
C = FiniteSet(1, 2, 3)
C
# In[15]:
# Generando el conjunto potencia. Esto no se puede
# hacer utilizando el conjunto por defecto de python.
C.powerset()
# In[16]:
# Cardinalidad
print("La cardinalidad del conjunto potencia del conjunto C = {0} es {1}".
format(C, len(C.powerset())))
# In[17]:
# Igualdad
A = FiniteSet(1, 2, 3)
B = FiniteSet(1, 3, 2)
A == B
# In[18]:
A = FiniteSet(1, 2, 3)
B = FiniteSet(1, 3, 4)
A == B
# In[19]:
# Subconjunto y subconjunto propio
A = FiniteSet(1,2,3)
B = FiniteSet(1,2,3,4,5)
A.is_subset(B)
# In[20]:
A.is_proper_subset(B)
# In[21]:
# A == B. El test de subconjunto propio da falso
B = FiniteSet(2,1,3)
A.is_proper_subset(B)
# In[22]:
# Union de dos conjuntos
A = FiniteSet(1, 2, 3)
B = FiniteSet(2, 4, 6)
A.union(B)
# In[23]:
# Interseccion de dos conjuntos
A = FiniteSet(1, 2)
B = FiniteSet(2, 3)
A.intersect(B)
# In[24]:
# Diferencia entre conjuntos
A - B
# In[25]:
# Calculando el producto cartesiano. Con el conjunto por
# defecto de python no podemos hacer esto con el operador *
A = FiniteSet(1, 2)
B = FiniteSet(3, 4)
P = A * B
P
# In[26]:
for elem in P:
print(elem)
# In[27]:
# Elevar a la n potencia un conjunto. Calcula el n
# producto cartesiano del mismo conjunto.
A = FiniteSet(1, 2, 3, 4)
P2 = A ** 2
P2
# In[28]:
P3 = A ** 3
P3
# In[29]:
for elem in P3:
print(elem)
# In[30]:
# graficos embebidos
get_ipython().run_line_magic('matplotlib', 'inline')
# In[31]:
# Dibujanto el diagrama de venn de 2 conjuntos
from matplotlib_venn import venn2, venn2_circles
import matplotlib.pyplot as plt
A = FiniteSet(1, 3, 5, 7, 9, 11, 13, 15, 17, 19)
B = FiniteSet(2, 3, 5, 7, 11, 13, 17, 19, 8)
plt.figure(figsize=(6, 8))
v = venn2(subsets=[A, B], set_labels=('A', 'B'))
v.get_label_by_id('10').set_text(A - B)
v.get_label_by_id('11').set_text(A.intersection(B))
v.get_label_by_id('01').set_text(B - A)
c = venn2_circles(subsets=[A, B], linestyle='dashed')
c[0].set_ls('solid')
plt.show()
# Además de las aplicaciones que pueden tener los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) de [Python](https://www.python.org/) en matemáticas, los mismos también pueden ser una [estructura de datos](https://es.wikipedia.org/wiki/Estructura_de_datos) poderosa y ayudarnos a resolver varios problemas de programación en forma muy sencilla. A tenerlos en cuenta!
#
# Con esto termino este artículo; espero que les haya gustado y les sea de utilidad.
# Saludos!
#
# *Este post fue escrito utilizando IPython notebook. Pueden descargar este [notebook](https://github.com/relopezbriega/relopezbriega.github.io/blob/master/downloads/pythonSets.ipynb) o ver su version estática en [nbviewer](http://nbviewer.ipython.org/github/relopezbriega/relopezbriega.github.io/blob/master/downloads/pythonSets.ipynb).*
 # ## Introducción
#
# Una característica notable de los seres humanos es su inherente necesidad y capacidad de agrupar objetos de acuerdo a criterios específicos.
# La idea de la clasificación de ciertos objetos en grupos similares, o *[conjuntos](https://es.wikipedia.org/wiki/Conjunto)*, es uno de los conceptos más fundamentales de la matemática moderna. La [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos) ha sido el marco unificador para todas las matemáticas desde que el matemático alemán [Georg Cantor](https://es.wikipedia.org/wiki/Georg_Cantor) la formulara alrededor de 1870. Ningún campo de las matemáticas podría describirse hoy en día sin hacer referencia a algún tipo de [conjunto](https://es.wikipedia.org/wiki/Conjunto) abstracto.
# En términos más generales, el concepto de *membresía* de un [conjunto](https://es.wikipedia.org/wiki/Conjunto), que se encuentra en el corazón de la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos), explica cómo sentencias con sustantivos y predicados son formulados en nuestro lenguaje, o en cualquier lenguaje abstracto como las matemáticas. Debido a esto, la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos) está íntimamente ligada a la [lógica](https://es.wikipedia.org/wiki/L%C3%B3gica) y sirve de base para todas las matemáticas.
#
# ## ¿Qué es un conjunto?
#
# **Un [conjunto](https://es.wikipedia.org/wiki/Conjunto) es una colección de objetos distintos, a menudo llamados elementos o miembros**. Existen dos características hacen de los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) algo totalmente distinto a cualquier otra colección de objetos. En primer lugar, un [conjunto](https://es.wikipedia.org/wiki/Conjunto) está siempre "bien definido", es decir que si realizamos la pregunta *¿Este objeto particular, se encuentra en esta colección?*; siempre debe existir una respuesta clara por sí o por no basada en una regla o algunos criterios dados. La segunda característica, es que no hay dos miembros de
# un mismo [conjunto](https://es.wikipedia.org/wiki/Conjunto) que sean exactamente iguales, es decir, que no hay elementos repetidos.
# Un [conjunto](https://es.wikipedia.org/wiki/Conjunto) puede contener cualquier cosa imaginable, incluyendo números, letras, colores, incluso otros [conjuntos](https://es.wikipedia.org/wiki/Conjunto)!. Sin embargo, ninguno de los objetos del [conjunto](https://es.wikipedia.org/wiki/Conjunto) puede ser el propio [conjunto](https://es.wikipedia.org/wiki/Conjunto). Descartamos esta posibilidad para evitar encontrarnos con la [Paradoja de Russell](https://es.wikipedia.org/wiki/Paradoja_de_Russell), un problema famoso en la lógica matemática desenterrado por el gran lógico británico [Bertrand Russell](https://es.wikipedia.org/wiki/Bertrand_Russell) en 1901.
#
# ## Notación de Conjuntos
#
# Cuando escribimos a los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) utilizamos letras mayúsculas para sus nombres y para representar al [conjunto](https://es.wikipedia.org/wiki/Conjunto) propiamente dicho simplemente listamos sus elementos separándolos por comas y luego englobamos todos estos elementos dentro de un par de llaves. Así, por ejemplo, A = {1,2,3, ..., 10} es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de los 10 primeros [números naturales](https://es.wikipedia.org/wiki/N%C3%BAmero_natural) o para *contar*, B = {Rojo, Azul, Verde} es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de colores primarios, N = {1,2,3, ...} es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de todos los [números naturales](https://es.wikipedia.org/wiki/N%C3%BAmero_natural), y Z = {..., - 3, -2, -1,0,1,2,3, ...}
# es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de todos los [números enteros](https://es.wikipedia.org/wiki/N%C3%BAmero_entero). Los puntos suspensivos "..." se utilizan para describir el carácter *infinito* de los números en los conjuntos N y Z.
#
# También se utiliza el símbolo $ \in $ para expresar que determina objeto pertenece o es *miembro* de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) y el símbolo $ \notin $ para indicar que no pertenece a un [conjunto](https://es.wikipedia.org/wiki/Conjunto). Utilizando los ejemplos anteriores, podríamos por ejemplo escribir que $7 \in A$ y $12 \notin A$.
#
# Dado que muchos [conjuntos](https://es.wikipedia.org/wiki/Conjunto) no se pueden describir listando todos sus miembros, ya que en muchos casos esto es imposible, también se utiliza la mucho más potente notación de constructor de conjuntos o predicado. En esta notación escribimos el conjunto de acuerdo a qué tipos de objetos pertenecen al [conjunto](https://es.wikipedia.org/wiki/Conjunto), que se colocan a la izquierda del símbolo "|", que significa "de tal manera que," dentro de las llaves; así como las condiciones que estos objetos deben cumplir para pertenecer al [conjunto](https://es.wikipedia.org/wiki/Conjunto), las cuales se colocan a la derecha de "|" dentro de las llaves. Por ejemplo, el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de los [números racionales](https://es.wikipedia.org/wiki/N%C3%BAmero_racional), o fracciones, que se denota por Q no puede ser descrito por el método de listar todos sus miembros. En su lugar, se define a Q utilizando la notación de predicado de la siguiente manera:
# $Q=\{\frac{p}{q} \mid p, q \in Z$ y $q \ne 0 \}$
# Esto se lee "Q es el conjunto de todas las fracciones de la forma p sobre q, tal que p y q son números enteros y q no es cero." También podríamos escribir al conjunto A de nuestro ejemplo anterior como $A = \{x \mid x \in N$ y
# $x < 11\}$.
#
# ## Conjuntos numéricos
#
# Dentro de las matemáticas, los principales [conjuntos](https://es.wikipedia.org/wiki/Conjunto) numéricos que podemos encontrar y que tienen un carácter universal son:
#
# * $\mathbb{N} = \{1,2,3, ...\}$ es el conjunto de los [números naturales](https://es.wikipedia.org/wiki/N%C3%BAmero_natural).
# * $\mathbb{W} = \{0,1,2,3, ...\}$ es el conjunto de los [números enteros](https://es.wikipedia.org/wiki/N%C3%BAmero_entero) positivos.
# * $\mathbb{Z} = \{...,-3,-2,-1,0,1,2,3, ...\}$ es el conjunto de todos los [números enteros](https://es.wikipedia.org/wiki/N%C3%BAmero_entero).
# * $\mathbb{Q} =\{\frac{p}{q} \mid p, q \in Z$ y $q \ne 0 \}$ es el conjunto de los [números racionales](https://es.wikipedia.org/wiki/N%C3%BAmero_racional).
# * $\mathbb{R}$, es el conjunto de los [números reales](https://es.wikipedia.org/wiki/N%C3%BAmero_real). Estos son todos los números que pueden ser colocados en una recta numérica unidimensional que se extiende sin fin tanto en negativo como positivo.
# * $\mathbb{I}$, es el conjunto de los [números irracionales](https://es.wikipedia.org/wiki/N%C3%BAmero_irracional). Algunos de los números más importantes en matemáticas pertenecen a este conjunto,incluyendo $\pi, \sqrt{2}, e$ y $\phi$.
# * $\mathbb{C}$, es el conjunto de los [números complejos](https://es.wikipedia.org/wiki/N%C3%BAmero_complejo). Estos son los números que contienen una parte real y otra parte imaginaria.
#
# ## Igualdad entre conjuntos
#
# El concepto de igualdad en los [conjuntos](https://es.wikipedia.org/wiki/Conjunto), difiere levemente del clásico concepto de igualdad que solemos tener. Dos conjuntos A y B se dice que son iguales (expresado por A = B), si y sólo si ambos [conjuntos](https://es.wikipedia.org/wiki/Conjunto) tienen exactamente los mismos elementos. Por ejemplo el [conjunto](https://es.wikipedia.org/wiki/Conjunto) A={1,2,3,4} es igual al [conjunto](https://es.wikipedia.org/wiki/Conjunto) B={4,3,2,1}.
# Un [conjunto](https://es.wikipedia.org/wiki/Conjunto) importante, y que todavía no hemos mencionado es el **[conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo)**, el cual no tiene elementos y por tanto no puede ser igualado con ningún otro [conjunto](https://es.wikipedia.org/wiki/Conjunto). Se expresa con el símbolo $\emptyset$ o {}.
#
# ## Cardinalidad
#
# La [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A es el número de elementos que pertenecen a A y lo expresamos como n(A). La [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) puede ser pensada tambien como una medida de su "tamaño". Si la [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) es un [número entero](https://es.wikipedia.org/wiki/N%C3%BAmero_entero), entonces el conjunto se dice que es finito. De lo contrario, el conjunto se dice que es infinito. Así por ejemplo la [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) del [conjunto](https://es.wikipedia.org/wiki/Conjunto) A={1,2,...,9,10} es 10 y lo expresamos como n(A)=10.
#
# ## Subconjunto y subconjunto propio
#
# Si todos los elementos de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A son también elementos de otro [conjunto](https://es.wikipedia.org/wiki/Conjunto) B, entonces A se llama un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) de B y lo expresamos como $A \subseteq B$. En cierto sentido, se puede
# pensar al [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) A como dentro, o contenido en el [conjunto](https://es.wikipedia.org/wiki/Conjunto) B.
# Si un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A es un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) de B y los dos [conjuntos](https://es.wikipedia.org/wiki/Conjunto) no son iguales, entonces llamamos A un [subconjunto propio](https://es.wikipedia.org/wiki/Subconjunto#Subconjunto_propio) de B y lo expresamos como $A \subset B$. En este caso, se dice que el [conjunto](https://es.wikipedia.org/wiki/Conjunto) A esta propiamente contenido en B.
# Algunas propiedades importantes relacionadas con [subconjuntos](https://es.wikipedia.org/wiki/Subconjunto) y [subconjuntos propios](https://es.wikipedia.org/wiki/Subconjunto#Subconjunto_propio) son las siguientes:
#
# * Cualquier [conjunto](https://es.wikipedia.org/wiki/Conjunto) A es un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) de sí mismo. Por lo tanto $A \subseteq A$. Esto es claramente cierto.
# * Menos obvio es el hecho de que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) es un subconjunto de cualquier conjunto A. Por lo tanto $\emptyset \subseteq A$. Esta propiedad se prueba a través de la contradicción, ya que si asumimos que existe un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A del que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) no es un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto), entonces esto quiere decir que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) debe contener un elemento que no se encuentra en A y esto es absurdo ya que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) no contiene ningún elemento.
# * El [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) es un [subconjunto propio](https://es.wikipedia.org/wiki/Subconjunto#Subconjunto_propio) de cualquier [conjunto](https://es.wikipedia.org/wiki/Conjunto) A, siempre y cuando A no se también un [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo).
# * Para los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) finitos A y B, si $A \subseteq B$, entonces $n(A) \leq n(B)$.
# * De forma similar, para los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) finitos A y B, si $A \subset B$, entonces $n(A) < n(B)$.
#
#
# ## Conjunto potencia
#
# El [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A, expresado por $P_{A}$, es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) formado por todos los distintos [subconjuntos](https://es.wikipedia.org/wiki/Subconjunto) de A. Así por ejemplo el [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) del [conjunto](https://es.wikipedia.org/wiki/Conjunto) $A=\{1,2,3\}$; va a ser igual a $P_{A}=\{\emptyset,\{1\},\{2\},\{3\},\{1,2\},\{2,3\}, \{1,3\},\{1,2,3\}\}$.
#
# Un teorema importante de la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos) establece que si A es un [conjunto](https://es.wikipedia.org/wiki/Conjunto) con k elementos, es decir que n(A) = k; entonces el [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) de A tiene exactamente $2^k$ elementos. Escribimos esto como $n(P_{A}) = 2^k$. En nuestro ejemplo anterior podemos ver que n(A)=3, por lo tanto $n(P_{A}) = 2^3$, lo que es igual a los 8 elementos que vimos que tiene el [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) de A.
#
# ## Algebra de conjuntos
#
# El [álgebra de conjuntos](https://es.wikipedia.org/wiki/%C3%81lgebra_de_conjuntos) es el estudio de las operaciones básicas que podemos realizar con los [conjuntos](https://es.wikipedia.org/wiki/Conjunto). Las operaciones básicas del álgebra de conjuntos son:
#
# * **Unión**. La [unión](https://es.wikipedia.org/wiki/Uni%C3%B3n_de_conjuntos) de dos conjuntos A y B es el conjunto $A \cup B$ que contiene todos los elementos de A y de B.
#
# ## Introducción
#
# Una característica notable de los seres humanos es su inherente necesidad y capacidad de agrupar objetos de acuerdo a criterios específicos.
# La idea de la clasificación de ciertos objetos en grupos similares, o *[conjuntos](https://es.wikipedia.org/wiki/Conjunto)*, es uno de los conceptos más fundamentales de la matemática moderna. La [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos) ha sido el marco unificador para todas las matemáticas desde que el matemático alemán [Georg Cantor](https://es.wikipedia.org/wiki/Georg_Cantor) la formulara alrededor de 1870. Ningún campo de las matemáticas podría describirse hoy en día sin hacer referencia a algún tipo de [conjunto](https://es.wikipedia.org/wiki/Conjunto) abstracto.
# En términos más generales, el concepto de *membresía* de un [conjunto](https://es.wikipedia.org/wiki/Conjunto), que se encuentra en el corazón de la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos), explica cómo sentencias con sustantivos y predicados son formulados en nuestro lenguaje, o en cualquier lenguaje abstracto como las matemáticas. Debido a esto, la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos) está íntimamente ligada a la [lógica](https://es.wikipedia.org/wiki/L%C3%B3gica) y sirve de base para todas las matemáticas.
#
# ## ¿Qué es un conjunto?
#
# **Un [conjunto](https://es.wikipedia.org/wiki/Conjunto) es una colección de objetos distintos, a menudo llamados elementos o miembros**. Existen dos características hacen de los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) algo totalmente distinto a cualquier otra colección de objetos. En primer lugar, un [conjunto](https://es.wikipedia.org/wiki/Conjunto) está siempre "bien definido", es decir que si realizamos la pregunta *¿Este objeto particular, se encuentra en esta colección?*; siempre debe existir una respuesta clara por sí o por no basada en una regla o algunos criterios dados. La segunda característica, es que no hay dos miembros de
# un mismo [conjunto](https://es.wikipedia.org/wiki/Conjunto) que sean exactamente iguales, es decir, que no hay elementos repetidos.
# Un [conjunto](https://es.wikipedia.org/wiki/Conjunto) puede contener cualquier cosa imaginable, incluyendo números, letras, colores, incluso otros [conjuntos](https://es.wikipedia.org/wiki/Conjunto)!. Sin embargo, ninguno de los objetos del [conjunto](https://es.wikipedia.org/wiki/Conjunto) puede ser el propio [conjunto](https://es.wikipedia.org/wiki/Conjunto). Descartamos esta posibilidad para evitar encontrarnos con la [Paradoja de Russell](https://es.wikipedia.org/wiki/Paradoja_de_Russell), un problema famoso en la lógica matemática desenterrado por el gran lógico británico [Bertrand Russell](https://es.wikipedia.org/wiki/Bertrand_Russell) en 1901.
#
# ## Notación de Conjuntos
#
# Cuando escribimos a los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) utilizamos letras mayúsculas para sus nombres y para representar al [conjunto](https://es.wikipedia.org/wiki/Conjunto) propiamente dicho simplemente listamos sus elementos separándolos por comas y luego englobamos todos estos elementos dentro de un par de llaves. Así, por ejemplo, A = {1,2,3, ..., 10} es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de los 10 primeros [números naturales](https://es.wikipedia.org/wiki/N%C3%BAmero_natural) o para *contar*, B = {Rojo, Azul, Verde} es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de colores primarios, N = {1,2,3, ...} es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de todos los [números naturales](https://es.wikipedia.org/wiki/N%C3%BAmero_natural), y Z = {..., - 3, -2, -1,0,1,2,3, ...}
# es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de todos los [números enteros](https://es.wikipedia.org/wiki/N%C3%BAmero_entero). Los puntos suspensivos "..." se utilizan para describir el carácter *infinito* de los números en los conjuntos N y Z.
#
# También se utiliza el símbolo $ \in $ para expresar que determina objeto pertenece o es *miembro* de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) y el símbolo $ \notin $ para indicar que no pertenece a un [conjunto](https://es.wikipedia.org/wiki/Conjunto). Utilizando los ejemplos anteriores, podríamos por ejemplo escribir que $7 \in A$ y $12 \notin A$.
#
# Dado que muchos [conjuntos](https://es.wikipedia.org/wiki/Conjunto) no se pueden describir listando todos sus miembros, ya que en muchos casos esto es imposible, también se utiliza la mucho más potente notación de constructor de conjuntos o predicado. En esta notación escribimos el conjunto de acuerdo a qué tipos de objetos pertenecen al [conjunto](https://es.wikipedia.org/wiki/Conjunto), que se colocan a la izquierda del símbolo "|", que significa "de tal manera que," dentro de las llaves; así como las condiciones que estos objetos deben cumplir para pertenecer al [conjunto](https://es.wikipedia.org/wiki/Conjunto), las cuales se colocan a la derecha de "|" dentro de las llaves. Por ejemplo, el [conjunto](https://es.wikipedia.org/wiki/Conjunto) de los [números racionales](https://es.wikipedia.org/wiki/N%C3%BAmero_racional), o fracciones, que se denota por Q no puede ser descrito por el método de listar todos sus miembros. En su lugar, se define a Q utilizando la notación de predicado de la siguiente manera:
# $Q=\{\frac{p}{q} \mid p, q \in Z$ y $q \ne 0 \}$
# Esto se lee "Q es el conjunto de todas las fracciones de la forma p sobre q, tal que p y q son números enteros y q no es cero." También podríamos escribir al conjunto A de nuestro ejemplo anterior como $A = \{x \mid x \in N$ y
# $x < 11\}$.
#
# ## Conjuntos numéricos
#
# Dentro de las matemáticas, los principales [conjuntos](https://es.wikipedia.org/wiki/Conjunto) numéricos que podemos encontrar y que tienen un carácter universal son:
#
# * $\mathbb{N} = \{1,2,3, ...\}$ es el conjunto de los [números naturales](https://es.wikipedia.org/wiki/N%C3%BAmero_natural).
# * $\mathbb{W} = \{0,1,2,3, ...\}$ es el conjunto de los [números enteros](https://es.wikipedia.org/wiki/N%C3%BAmero_entero) positivos.
# * $\mathbb{Z} = \{...,-3,-2,-1,0,1,2,3, ...\}$ es el conjunto de todos los [números enteros](https://es.wikipedia.org/wiki/N%C3%BAmero_entero).
# * $\mathbb{Q} =\{\frac{p}{q} \mid p, q \in Z$ y $q \ne 0 \}$ es el conjunto de los [números racionales](https://es.wikipedia.org/wiki/N%C3%BAmero_racional).
# * $\mathbb{R}$, es el conjunto de los [números reales](https://es.wikipedia.org/wiki/N%C3%BAmero_real). Estos son todos los números que pueden ser colocados en una recta numérica unidimensional que se extiende sin fin tanto en negativo como positivo.
# * $\mathbb{I}$, es el conjunto de los [números irracionales](https://es.wikipedia.org/wiki/N%C3%BAmero_irracional). Algunos de los números más importantes en matemáticas pertenecen a este conjunto,incluyendo $\pi, \sqrt{2}, e$ y $\phi$.
# * $\mathbb{C}$, es el conjunto de los [números complejos](https://es.wikipedia.org/wiki/N%C3%BAmero_complejo). Estos son los números que contienen una parte real y otra parte imaginaria.
#
# ## Igualdad entre conjuntos
#
# El concepto de igualdad en los [conjuntos](https://es.wikipedia.org/wiki/Conjunto), difiere levemente del clásico concepto de igualdad que solemos tener. Dos conjuntos A y B se dice que son iguales (expresado por A = B), si y sólo si ambos [conjuntos](https://es.wikipedia.org/wiki/Conjunto) tienen exactamente los mismos elementos. Por ejemplo el [conjunto](https://es.wikipedia.org/wiki/Conjunto) A={1,2,3,4} es igual al [conjunto](https://es.wikipedia.org/wiki/Conjunto) B={4,3,2,1}.
# Un [conjunto](https://es.wikipedia.org/wiki/Conjunto) importante, y que todavía no hemos mencionado es el **[conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo)**, el cual no tiene elementos y por tanto no puede ser igualado con ningún otro [conjunto](https://es.wikipedia.org/wiki/Conjunto). Se expresa con el símbolo $\emptyset$ o {}.
#
# ## Cardinalidad
#
# La [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A es el número de elementos que pertenecen a A y lo expresamos como n(A). La [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) puede ser pensada tambien como una medida de su "tamaño". Si la [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) es un [número entero](https://es.wikipedia.org/wiki/N%C3%BAmero_entero), entonces el conjunto se dice que es finito. De lo contrario, el conjunto se dice que es infinito. Así por ejemplo la [cardinalidad](https://es.wikipedia.org/wiki/Conjunto#Cardinalidad) del [conjunto](https://es.wikipedia.org/wiki/Conjunto) A={1,2,...,9,10} es 10 y lo expresamos como n(A)=10.
#
# ## Subconjunto y subconjunto propio
#
# Si todos los elementos de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A son también elementos de otro [conjunto](https://es.wikipedia.org/wiki/Conjunto) B, entonces A se llama un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) de B y lo expresamos como $A \subseteq B$. En cierto sentido, se puede
# pensar al [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) A como dentro, o contenido en el [conjunto](https://es.wikipedia.org/wiki/Conjunto) B.
# Si un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A es un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) de B y los dos [conjuntos](https://es.wikipedia.org/wiki/Conjunto) no son iguales, entonces llamamos A un [subconjunto propio](https://es.wikipedia.org/wiki/Subconjunto#Subconjunto_propio) de B y lo expresamos como $A \subset B$. En este caso, se dice que el [conjunto](https://es.wikipedia.org/wiki/Conjunto) A esta propiamente contenido en B.
# Algunas propiedades importantes relacionadas con [subconjuntos](https://es.wikipedia.org/wiki/Subconjunto) y [subconjuntos propios](https://es.wikipedia.org/wiki/Subconjunto#Subconjunto_propio) son las siguientes:
#
# * Cualquier [conjunto](https://es.wikipedia.org/wiki/Conjunto) A es un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto) de sí mismo. Por lo tanto $A \subseteq A$. Esto es claramente cierto.
# * Menos obvio es el hecho de que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) es un subconjunto de cualquier conjunto A. Por lo tanto $\emptyset \subseteq A$. Esta propiedad se prueba a través de la contradicción, ya que si asumimos que existe un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A del que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) no es un [subconjunto](https://es.wikipedia.org/wiki/Subconjunto), entonces esto quiere decir que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) debe contener un elemento que no se encuentra en A y esto es absurdo ya que el [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) no contiene ningún elemento.
# * El [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo) es un [subconjunto propio](https://es.wikipedia.org/wiki/Subconjunto#Subconjunto_propio) de cualquier [conjunto](https://es.wikipedia.org/wiki/Conjunto) A, siempre y cuando A no se también un [conjunto vacío](https://es.wikipedia.org/wiki/Conjunto_vac%C3%ADo).
# * Para los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) finitos A y B, si $A \subseteq B$, entonces $n(A) \leq n(B)$.
# * De forma similar, para los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) finitos A y B, si $A \subset B$, entonces $n(A) < n(B)$.
#
#
# ## Conjunto potencia
#
# El [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) de un [conjunto](https://es.wikipedia.org/wiki/Conjunto) A, expresado por $P_{A}$, es el [conjunto](https://es.wikipedia.org/wiki/Conjunto) formado por todos los distintos [subconjuntos](https://es.wikipedia.org/wiki/Subconjunto) de A. Así por ejemplo el [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) del [conjunto](https://es.wikipedia.org/wiki/Conjunto) $A=\{1,2,3\}$; va a ser igual a $P_{A}=\{\emptyset,\{1\},\{2\},\{3\},\{1,2\},\{2,3\}, \{1,3\},\{1,2,3\}\}$.
#
# Un teorema importante de la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos) establece que si A es un [conjunto](https://es.wikipedia.org/wiki/Conjunto) con k elementos, es decir que n(A) = k; entonces el [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) de A tiene exactamente $2^k$ elementos. Escribimos esto como $n(P_{A}) = 2^k$. En nuestro ejemplo anterior podemos ver que n(A)=3, por lo tanto $n(P_{A}) = 2^3$, lo que es igual a los 8 elementos que vimos que tiene el [conjunto potencia](https://es.wikipedia.org/wiki/Conjunto_potencia) de A.
#
# ## Algebra de conjuntos
#
# El [álgebra de conjuntos](https://es.wikipedia.org/wiki/%C3%81lgebra_de_conjuntos) es el estudio de las operaciones básicas que podemos realizar con los [conjuntos](https://es.wikipedia.org/wiki/Conjunto). Las operaciones básicas del álgebra de conjuntos son:
#
# * **Unión**. La [unión](https://es.wikipedia.org/wiki/Uni%C3%B3n_de_conjuntos) de dos conjuntos A y B es el conjunto $A \cup B$ que contiene todos los elementos de A y de B.
#  #
# * **Intersección**. La [intersección](https://es.wikipedia.org/wiki/Intersecci%C3%B3n_de_conjuntos) de dos conjuntos A y B es el conjunto $A \cap B$ que contiene todos los elementos comunes de A y B.
#
#
# * **Intersección**. La [intersección](https://es.wikipedia.org/wiki/Intersecci%C3%B3n_de_conjuntos) de dos conjuntos A y B es el conjunto $A \cap B$ que contiene todos los elementos comunes de A y B.
#  #
# * **Diferencia**. La [diferencia](https://es.wikipedia.org/wiki/Diferencia_de_conjuntos) entre dos conjuntos A y B es el conjunto $A \setminus B$ que contiene todos los elementos de A que no pertenecen a B.
#
#
# * **Diferencia**. La [diferencia](https://es.wikipedia.org/wiki/Diferencia_de_conjuntos) entre dos conjuntos A y B es el conjunto $A \setminus B$ que contiene todos los elementos de A que no pertenecen a B.
#  #
# * **Complemento**. El [complemento](https://es.wikipedia.org/wiki/Complemento_de_un_conjunto) de un conjunto A es el conjunto $A^∁$ que contiene todos los elementos que no pertenecen a A.
#
#
# * **Complemento**. El [complemento](https://es.wikipedia.org/wiki/Complemento_de_un_conjunto) de un conjunto A es el conjunto $A^∁$ que contiene todos los elementos que no pertenecen a A.
#  #
# * **Producto cartesiano**. El [producto cartesiano](https://es.wikipedia.org/wiki/Producto_cartesiano) de dos conjuntos A y B es el conjunto $A \times B$ que contiene todos los pares ordenados (a, b) cuyo primer elemento pertenece a A y su segundo elemento pertenece a B.
#
#
# ## Conjuntos con Python
#
# Luego de todo este repaso por los fundamentos de la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos), es tiempo de ver como podemos utilizar a los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) dentro de [Python](https://www.python.org/); ya que el lenguaje trae como una de sus [estructuras de datos](https://es.wikipedia.org/wiki/Estructura_de_datos) por defecto a los [conjuntos](https://es.wikipedia.org/wiki/Conjunto). También veremos que podemos utilizar el *constructor* `FiniteSet` que nos proporciona [sympy](http://www.sympy.org/es/), el cual tiene ciertas ventajas sobre la versión por defecto de [Python](https://www.python.org/).
# In[1]:
# Creando un conjunto en python
A = {1,2,3}
A
# In[2]:
# Creando un conjunto a partir de una lista
lista = ["bananas", "manzanas", "naranjas", "limones"]
B = set(lista)
B
# In[3]:
# Los conjuntos eliminan los elementos duplicados
lista = ["bananas", "manzanas", "naranjas", "limones",
"bananas", "bananas", "limones", "naranjas"]
B = set(lista)
B
# In[4]:
# Creando el conjunto vacío
O = set()
O
# In[5]:
# Cardinalidad de un conjunto con len().
print("La cardinalidad del conjunto A = {0} es {1}".format(A,len(A)))
# In[6]:
# comprobando membresía
2 in A
# In[7]:
# Igualdad entre conjuntos. El orden de los elementos no importa.
A = {1,2,3,4}
B = {4,2,3,1}
A == B
# In[8]:
# Subconjunto. No hay distincion entre subconjunto y propio
# para el conjunto por defecto de python.
A = {1,2,3}
B = {1,2,3,4,5}
A.issubset(B)
# In[9]:
# Subconjunto propio
A.issubset(B) and A != B
# In[10]:
# Union de conjuntos
A = {1,2,3,4,5}
B = {4,5,6,7,8,9,10}
A.union(B)
# In[11]:
# Intersección de conjuntos
A.intersection(B)
# In[12]:
# Diferencia entre conjuntos
A - B
# In[13]:
B - A
# In[14]:
# Utilizando FiniteSet de sympy
from sympy import FiniteSet
C = FiniteSet(1, 2, 3)
C
# In[15]:
# Generando el conjunto potencia. Esto no se puede
# hacer utilizando el conjunto por defecto de python.
C.powerset()
# In[16]:
# Cardinalidad
print("La cardinalidad del conjunto potencia del conjunto C = {0} es {1}".
format(C, len(C.powerset())))
# In[17]:
# Igualdad
A = FiniteSet(1, 2, 3)
B = FiniteSet(1, 3, 2)
A == B
# In[18]:
A = FiniteSet(1, 2, 3)
B = FiniteSet(1, 3, 4)
A == B
# In[19]:
# Subconjunto y subconjunto propio
A = FiniteSet(1,2,3)
B = FiniteSet(1,2,3,4,5)
A.is_subset(B)
# In[20]:
A.is_proper_subset(B)
# In[21]:
# A == B. El test de subconjunto propio da falso
B = FiniteSet(2,1,3)
A.is_proper_subset(B)
# In[22]:
# Union de dos conjuntos
A = FiniteSet(1, 2, 3)
B = FiniteSet(2, 4, 6)
A.union(B)
# In[23]:
# Interseccion de dos conjuntos
A = FiniteSet(1, 2)
B = FiniteSet(2, 3)
A.intersect(B)
# In[24]:
# Diferencia entre conjuntos
A - B
# In[25]:
# Calculando el producto cartesiano. Con el conjunto por
# defecto de python no podemos hacer esto con el operador *
A = FiniteSet(1, 2)
B = FiniteSet(3, 4)
P = A * B
P
# In[26]:
for elem in P:
print(elem)
# In[27]:
# Elevar a la n potencia un conjunto. Calcula el n
# producto cartesiano del mismo conjunto.
A = FiniteSet(1, 2, 3, 4)
P2 = A ** 2
P2
# In[28]:
P3 = A ** 3
P3
# In[29]:
for elem in P3:
print(elem)
# In[30]:
# graficos embebidos
get_ipython().run_line_magic('matplotlib', 'inline')
# In[31]:
# Dibujanto el diagrama de venn de 2 conjuntos
from matplotlib_venn import venn2, venn2_circles
import matplotlib.pyplot as plt
A = FiniteSet(1, 3, 5, 7, 9, 11, 13, 15, 17, 19)
B = FiniteSet(2, 3, 5, 7, 11, 13, 17, 19, 8)
plt.figure(figsize=(6, 8))
v = venn2(subsets=[A, B], set_labels=('A', 'B'))
v.get_label_by_id('10').set_text(A - B)
v.get_label_by_id('11').set_text(A.intersection(B))
v.get_label_by_id('01').set_text(B - A)
c = venn2_circles(subsets=[A, B], linestyle='dashed')
c[0].set_ls('solid')
plt.show()
# Además de las aplicaciones que pueden tener los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) de [Python](https://www.python.org/) en matemáticas, los mismos también pueden ser una [estructura de datos](https://es.wikipedia.org/wiki/Estructura_de_datos) poderosa y ayudarnos a resolver varios problemas de programación en forma muy sencilla. A tenerlos en cuenta!
#
# Con esto termino este artículo; espero que les haya gustado y les sea de utilidad.
# Saludos!
#
# *Este post fue escrito utilizando IPython notebook. Pueden descargar este [notebook](https://github.com/relopezbriega/relopezbriega.github.io/blob/master/downloads/pythonSets.ipynb) o ver su version estática en [nbviewer](http://nbviewer.ipython.org/github/relopezbriega/relopezbriega.github.io/blob/master/downloads/pythonSets.ipynb).*
#
# * **Producto cartesiano**. El [producto cartesiano](https://es.wikipedia.org/wiki/Producto_cartesiano) de dos conjuntos A y B es el conjunto $A \times B$ que contiene todos los pares ordenados (a, b) cuyo primer elemento pertenece a A y su segundo elemento pertenece a B.
#
#
# ## Conjuntos con Python
#
# Luego de todo este repaso por los fundamentos de la [teoría de conjuntos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_conjuntos), es tiempo de ver como podemos utilizar a los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) dentro de [Python](https://www.python.org/); ya que el lenguaje trae como una de sus [estructuras de datos](https://es.wikipedia.org/wiki/Estructura_de_datos) por defecto a los [conjuntos](https://es.wikipedia.org/wiki/Conjunto). También veremos que podemos utilizar el *constructor* `FiniteSet` que nos proporciona [sympy](http://www.sympy.org/es/), el cual tiene ciertas ventajas sobre la versión por defecto de [Python](https://www.python.org/).
# In[1]:
# Creando un conjunto en python
A = {1,2,3}
A
# In[2]:
# Creando un conjunto a partir de una lista
lista = ["bananas", "manzanas", "naranjas", "limones"]
B = set(lista)
B
# In[3]:
# Los conjuntos eliminan los elementos duplicados
lista = ["bananas", "manzanas", "naranjas", "limones",
"bananas", "bananas", "limones", "naranjas"]
B = set(lista)
B
# In[4]:
# Creando el conjunto vacío
O = set()
O
# In[5]:
# Cardinalidad de un conjunto con len().
print("La cardinalidad del conjunto A = {0} es {1}".format(A,len(A)))
# In[6]:
# comprobando membresía
2 in A
# In[7]:
# Igualdad entre conjuntos. El orden de los elementos no importa.
A = {1,2,3,4}
B = {4,2,3,1}
A == B
# In[8]:
# Subconjunto. No hay distincion entre subconjunto y propio
# para el conjunto por defecto de python.
A = {1,2,3}
B = {1,2,3,4,5}
A.issubset(B)
# In[9]:
# Subconjunto propio
A.issubset(B) and A != B
# In[10]:
# Union de conjuntos
A = {1,2,3,4,5}
B = {4,5,6,7,8,9,10}
A.union(B)
# In[11]:
# Intersección de conjuntos
A.intersection(B)
# In[12]:
# Diferencia entre conjuntos
A - B
# In[13]:
B - A
# In[14]:
# Utilizando FiniteSet de sympy
from sympy import FiniteSet
C = FiniteSet(1, 2, 3)
C
# In[15]:
# Generando el conjunto potencia. Esto no se puede
# hacer utilizando el conjunto por defecto de python.
C.powerset()
# In[16]:
# Cardinalidad
print("La cardinalidad del conjunto potencia del conjunto C = {0} es {1}".
format(C, len(C.powerset())))
# In[17]:
# Igualdad
A = FiniteSet(1, 2, 3)
B = FiniteSet(1, 3, 2)
A == B
# In[18]:
A = FiniteSet(1, 2, 3)
B = FiniteSet(1, 3, 4)
A == B
# In[19]:
# Subconjunto y subconjunto propio
A = FiniteSet(1,2,3)
B = FiniteSet(1,2,3,4,5)
A.is_subset(B)
# In[20]:
A.is_proper_subset(B)
# In[21]:
# A == B. El test de subconjunto propio da falso
B = FiniteSet(2,1,3)
A.is_proper_subset(B)
# In[22]:
# Union de dos conjuntos
A = FiniteSet(1, 2, 3)
B = FiniteSet(2, 4, 6)
A.union(B)
# In[23]:
# Interseccion de dos conjuntos
A = FiniteSet(1, 2)
B = FiniteSet(2, 3)
A.intersect(B)
# In[24]:
# Diferencia entre conjuntos
A - B
# In[25]:
# Calculando el producto cartesiano. Con el conjunto por
# defecto de python no podemos hacer esto con el operador *
A = FiniteSet(1, 2)
B = FiniteSet(3, 4)
P = A * B
P
# In[26]:
for elem in P:
print(elem)
# In[27]:
# Elevar a la n potencia un conjunto. Calcula el n
# producto cartesiano del mismo conjunto.
A = FiniteSet(1, 2, 3, 4)
P2 = A ** 2
P2
# In[28]:
P3 = A ** 3
P3
# In[29]:
for elem in P3:
print(elem)
# In[30]:
# graficos embebidos
get_ipython().run_line_magic('matplotlib', 'inline')
# In[31]:
# Dibujanto el diagrama de venn de 2 conjuntos
from matplotlib_venn import venn2, venn2_circles
import matplotlib.pyplot as plt
A = FiniteSet(1, 3, 5, 7, 9, 11, 13, 15, 17, 19)
B = FiniteSet(2, 3, 5, 7, 11, 13, 17, 19, 8)
plt.figure(figsize=(6, 8))
v = venn2(subsets=[A, B], set_labels=('A', 'B'))
v.get_label_by_id('10').set_text(A - B)
v.get_label_by_id('11').set_text(A.intersection(B))
v.get_label_by_id('01').set_text(B - A)
c = venn2_circles(subsets=[A, B], linestyle='dashed')
c[0].set_ls('solid')
plt.show()
# Además de las aplicaciones que pueden tener los [conjuntos](https://es.wikipedia.org/wiki/Conjunto) de [Python](https://www.python.org/) en matemáticas, los mismos también pueden ser una [estructura de datos](https://es.wikipedia.org/wiki/Estructura_de_datos) poderosa y ayudarnos a resolver varios problemas de programación en forma muy sencilla. A tenerlos en cuenta!
#
# Con esto termino este artículo; espero que les haya gustado y les sea de utilidad.
# Saludos!
#
# *Este post fue escrito utilizando IPython notebook. Pueden descargar este [notebook](https://github.com/relopezbriega/relopezbriega.github.io/blob/master/downloads/pythonSets.ipynb) o ver su version estática en [nbviewer](http://nbviewer.ipython.org/github/relopezbriega/relopezbriega.github.io/blob/master/downloads/pythonSets.ipynb).*