#!/usr/bin/env python
# coding: utf-8
# # De tíos, primos, teoremas y conjeturas
# *Esta notebook fue creada originalmente como un blog post por [Raúl E. López Briega](http://relopezbriega.com.ar/) en [Mi blog sobre Python](http://relopezbriega.github.io). El contenido esta bajo la licencia BSD.*
#  # ## El tío Petros y la conjetura
#
# Hace un tiempo atrás, quede atrapado en la lectura de la apasionante novela de Apostolos Doxiadis, [El tío Petros y la conjetura de Goldbach](http://www.amazon.es/El-tio-petros-conjetura-goldbach/dp/8440694903). La novela trata basicamente de la relación entre un joven, en busca de su vocación, y su tío, quien en el pasado fue un prodigio de las matemáticas, pero que luego se recluyó de su familia y de la comunidad científica consumido por el intento solitario de demostrar uno de los problemas abiertos más difíciles de la [teoría de números](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_n%C3%BAmeros), la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)*. Lo que más me sorprendió del problema que consumió la vida del querido tío Petros, es lo simple que es su enunciado; la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)* nos dice que ***"Todo número par mayor que 2 puede escribirse como suma de dos números primos."***
#
# Este enunciado, junto con la otra conjetura postulada por [Goldbach](https://es.wikipedia.org/wiki/Christian_Goldbach), conocida como la *[Conjetura debil de Goldbach](https://es.wikipedia.org/wiki/Conjetura_d%C3%A9bil_de_Goldbach)*, que nos dice que ***"Todo número impar mayor que 5 puede expresarse como suma de tres números primos."***; trae a colación el concepto de los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* como bloques constructores de los enteros.
# ## Los números primos
#
# Pero, ¿cómo es esto de que los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* pueden ser considerados como bloques constructores de los números enteros?
#
# Un *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* es un entero positivo que solo puede ser dividido en dos [factores](https://es.wikipedia.org/wiki/Divisibilidad) distintos, 1 y si mismo. De esta definición se desprende que el número 1 no es un *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* ya que solo puede ser dividido en un solo [factor](https://es.wikipedia.org/wiki/Divisibilidad); en cambio, el número 2 si es *[primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*, el único *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* que es par.
#
# La idea de que los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* pueden ser considerados como bloques constructores de los números enteros surge del enunciado del [Teorema fundamental de la aritmética](https://es.wikipedia.org/wiki/Teorema_fundamental_de_la_aritm%C3%A9tica) que nos dice que ***"Todo entero positivo puede ser representado de forma única como un producto de factores primos"***; así por ejemplo el número $28$ puede ser representado como $2^2 * 7$; o el $60$ como $2^2 * 3 * 5$. Este teorema es un concepto fundamental en [criptografía](https://es.wikipedia.org/wiki/Criptograf%C3%ADa), los principales algoritmos de cifrado que se utilizan hoy en día residen en la [factorización de primos](https://es.wikipedia.org/wiki/Factorizaci%C3%B3n_de_enteros), ya que es un proceso que requiere de mucho esfuerzo para calcularse mientras más grande sea el número que queremos factorizar.
#
# Otro aspecto interesante de los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* es que parecen surgir en forma aleatoria, hay veces que pueden aparecer en pares como (11, 13), (29, 31) o (59, 61) pero otras veces puede haber un largo intervalo entre ellos. Aún no se ha encontrado una formula que pueda predecir cual va a ser el próximo *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*. Como parece ser bastante difícil encontrar un patrón en los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*, el esfuerzo de los matemáticos paso de intentar encontrar un patrón a intentar comprender la distribución de los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* dentro de todos los enteros; es decir, intentar responder la pregunta de ¿Cuál es la probabilidad de que un número sea primo si elijo un número al azar en el rango de 0 a N?. Uno de los primeros en dar una respuesta bastante aproximada a esta pregunta fue [Gauss](https://es.wikipedia.org/wiki/Carl_Friedrich_Gauss), quien con tan solo 15 años de edad propuso la formula $\pi(x)\approx\frac{x}{ln(x)}$ para responder a esa pregunta.
#
# La formula propuesta [Gauss](https://es.wikipedia.org/wiki/Carl_Friedrich_Gauss) implica que a medida que los números se hacen cada vez más grandes, los
# *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* son cada vez más escasos. Esto es lo que se conoce como [teorema de los números primos](https://es.wikipedia.org/wiki/Teorema_de_los_n%C3%BAmeros_primos).
# A pesar de que los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* son cada vez más escasos mientras más grandes, siguen surgiendo indefinidamente, son infinitos; esto esta bien demostrado por el ya famoso [teorema de Euclides](https://es.wikipedia.org/wiki/Teorema_de_Euclides); quien incluyo una de las más bellas demostraciones de las matemáticas en su obra [Elementos](https://es.wikipedia.org/wiki/Elementos_de_Euclides) en el 300 AC.
#
# ### Encontrando los números primos
#
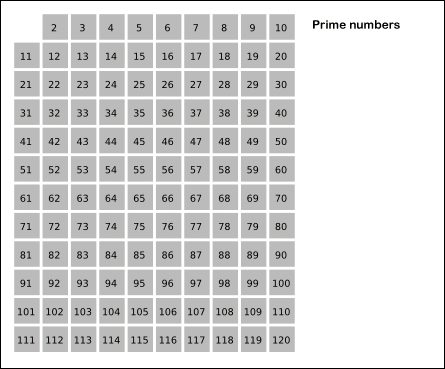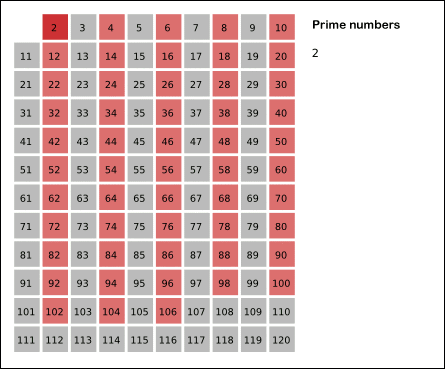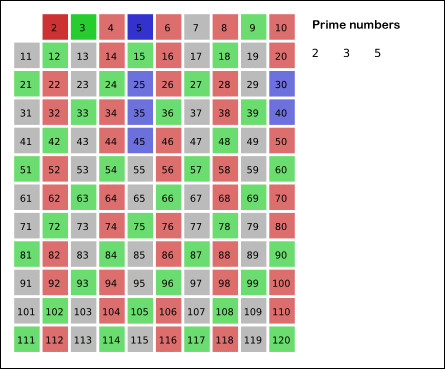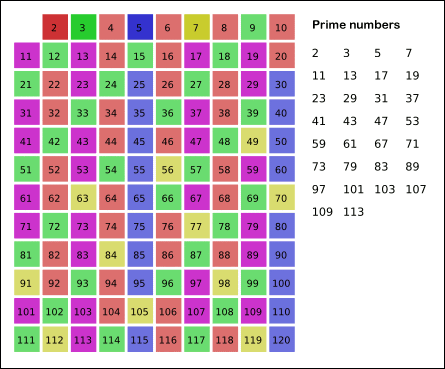
# Para encontrar todos los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* menores que un número N, uno de los algoritmos más eficientes y más fáciles de utilizar es lo que se conoce como la [criba de Eratóstenes](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes), el procedimiento que se utiliza consiste en crear una tabla con todos los números naturales comprendidos entre 2 y N, y luego ir tachando los números que no son primos de la siguiente manera: Comenzando por el 2, se tachan todos sus múltiplos; comenzando de nuevo, cuando se encuentra un número entero que no ha sido tachado, ese número es declarado primo, y se procede a tachar todos sus múltiplos, así sucesivamente. La siguiente animación describe el procedimiento graficamente.
#
# ## El tío Petros y la conjetura
#
# Hace un tiempo atrás, quede atrapado en la lectura de la apasionante novela de Apostolos Doxiadis, [El tío Petros y la conjetura de Goldbach](http://www.amazon.es/El-tio-petros-conjetura-goldbach/dp/8440694903). La novela trata basicamente de la relación entre un joven, en busca de su vocación, y su tío, quien en el pasado fue un prodigio de las matemáticas, pero que luego se recluyó de su familia y de la comunidad científica consumido por el intento solitario de demostrar uno de los problemas abiertos más difíciles de la [teoría de números](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_n%C3%BAmeros), la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)*. Lo que más me sorprendió del problema que consumió la vida del querido tío Petros, es lo simple que es su enunciado; la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)* nos dice que ***"Todo número par mayor que 2 puede escribirse como suma de dos números primos."***
#
# Este enunciado, junto con la otra conjetura postulada por [Goldbach](https://es.wikipedia.org/wiki/Christian_Goldbach), conocida como la *[Conjetura debil de Goldbach](https://es.wikipedia.org/wiki/Conjetura_d%C3%A9bil_de_Goldbach)*, que nos dice que ***"Todo número impar mayor que 5 puede expresarse como suma de tres números primos."***; trae a colación el concepto de los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* como bloques constructores de los enteros.
# ## Los números primos
#
# Pero, ¿cómo es esto de que los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* pueden ser considerados como bloques constructores de los números enteros?
#
# Un *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* es un entero positivo que solo puede ser dividido en dos [factores](https://es.wikipedia.org/wiki/Divisibilidad) distintos, 1 y si mismo. De esta definición se desprende que el número 1 no es un *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* ya que solo puede ser dividido en un solo [factor](https://es.wikipedia.org/wiki/Divisibilidad); en cambio, el número 2 si es *[primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*, el único *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* que es par.
#
# La idea de que los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* pueden ser considerados como bloques constructores de los números enteros surge del enunciado del [Teorema fundamental de la aritmética](https://es.wikipedia.org/wiki/Teorema_fundamental_de_la_aritm%C3%A9tica) que nos dice que ***"Todo entero positivo puede ser representado de forma única como un producto de factores primos"***; así por ejemplo el número $28$ puede ser representado como $2^2 * 7$; o el $60$ como $2^2 * 3 * 5$. Este teorema es un concepto fundamental en [criptografía](https://es.wikipedia.org/wiki/Criptograf%C3%ADa), los principales algoritmos de cifrado que se utilizan hoy en día residen en la [factorización de primos](https://es.wikipedia.org/wiki/Factorizaci%C3%B3n_de_enteros), ya que es un proceso que requiere de mucho esfuerzo para calcularse mientras más grande sea el número que queremos factorizar.
#
# Otro aspecto interesante de los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* es que parecen surgir en forma aleatoria, hay veces que pueden aparecer en pares como (11, 13), (29, 31) o (59, 61) pero otras veces puede haber un largo intervalo entre ellos. Aún no se ha encontrado una formula que pueda predecir cual va a ser el próximo *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*. Como parece ser bastante difícil encontrar un patrón en los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*, el esfuerzo de los matemáticos paso de intentar encontrar un patrón a intentar comprender la distribución de los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* dentro de todos los enteros; es decir, intentar responder la pregunta de ¿Cuál es la probabilidad de que un número sea primo si elijo un número al azar en el rango de 0 a N?. Uno de los primeros en dar una respuesta bastante aproximada a esta pregunta fue [Gauss](https://es.wikipedia.org/wiki/Carl_Friedrich_Gauss), quien con tan solo 15 años de edad propuso la formula $\pi(x)\approx\frac{x}{ln(x)}$ para responder a esa pregunta.
#
# La formula propuesta [Gauss](https://es.wikipedia.org/wiki/Carl_Friedrich_Gauss) implica que a medida que los números se hacen cada vez más grandes, los
# *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* son cada vez más escasos. Esto es lo que se conoce como [teorema de los números primos](https://es.wikipedia.org/wiki/Teorema_de_los_n%C3%BAmeros_primos).
# A pesar de que los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* son cada vez más escasos mientras más grandes, siguen surgiendo indefinidamente, son infinitos; esto esta bien demostrado por el ya famoso [teorema de Euclides](https://es.wikipedia.org/wiki/Teorema_de_Euclides); quien incluyo una de las más bellas demostraciones de las matemáticas en su obra [Elementos](https://es.wikipedia.org/wiki/Elementos_de_Euclides) en el 300 AC.
#
# ### Encontrando los números primos
#
# Para encontrar todos los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* menores que un número N, uno de los algoritmos más eficientes y más fáciles de utilizar es lo que se conoce como la [criba de Eratóstenes](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes), el procedimiento que se utiliza consiste en crear una tabla con todos los números naturales comprendidos entre 2 y N, y luego ir tachando los números que no son primos de la siguiente manera: Comenzando por el 2, se tachan todos sus múltiplos; comenzando de nuevo, cuando se encuentra un número entero que no ha sido tachado, ese número es declarado primo, y se procede a tachar todos sus múltiplos, así sucesivamente. La siguiente animación describe el procedimiento graficamente.
#  #
# ### Ejemplo en Python
#
# Veamos un ejemplo en [Python](https://www.python.org/) de como implementar la [criba de Eratóstenes](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes) y un proceso de [factorización de primos](https://es.wikipedia.org/wiki/Factorizaci%C3%B3n_de_enteros).
# In[1]:
# Factorizando primos en Python
import numpy as np
def criba_eratostenes(n):
"""Criba Eratostenes"""
l=[]
multiplos = set()
for i in range(2, n+1):
if i not in multiplos:
l.append(i)
multiplos.update(range(i*i, n+1, i))
return l
def factorizar_primos(n):
"""Factoriza un entero positivo en primos
>>>factorizar_primos(28)
[2, 2, 7]
"""
if n <=1:
return "Ingresar un entero mayor a 1"
factores = []
primos = criba_eratostenes(n)
pindex = 0
p = primos[pindex]
num = n
while p != num:
if num % p == 0:
factores.append(p)
num //= p
else:
pindex += 1
p = primos[pindex]
factores.append(p)
return factores
factorizar_primos(28) # Factores primos de 28
# In[2]:
# Factores primos de 1982
factorizar_primos(1982)
# In[3]:
# Factores primos de 2015
factorizar_primos(2015)
# ## La conjetura de Goldbach y Python
#
# La *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)*, es otro ejemplo de como también podemos construir todos los números enteros con simples operaciones aritméticas como la suma y no más que tres *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*. Al día de hoy, la [conjetura](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach) continua sin poder ser demostrada; y es considerada uno de los problemas más difíciles de las matemáticas. La mayoría de los matemáticos estiman que es verdadera, ya que se ha mostrado cierta hasta por lo menos el $10^{18}$; aunque algunos dudan que sea cierta para números extremadamente grandes, el gran [Ramanujan](https://es.wikipedia.org/wiki/Srinivasa_Aiyangar_Ramanujan) dicen que se incluía en este último grupo.
#
# Obviamente, como este blog esta dedicado a [Python](https://www.python.org/), no podría concluir este artículo sin incluir una implementación de la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)* en uno de los lenguajes que mejor se lleva con las matemáticas!
#
# En esta implementación vamos a utilizar tres funciones, en primer lugar una [criba de primos](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes) vectorizada utilizando [numpy](http://www.numpy.org/), para lograr un mejor rendimiento que con la [criba de Eratóstenes](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes) del ejemplo anterior; y luego vamos a tener dos sencillas funciones adicionales, una que nos devuelva la composición de Goldbach para cualquier número par que le pasemos como parámetro.(esta función solo nos va a devolver la primer solución que encuentra, ya que pueden existir varias soluciones para algunos enteros pares). Por último, la restante función va a listar los resultados de la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)* para un rango de números enteros.
# In[4]:
# La conjetura de Goldbach en Python
import numpy as np
def criba_primos(n):
"""Criba generadora de números primos.
Input n>=6, devuleve un array de primos, 2 <= p < n
"""
criba = np.ones(n / 3 + (n % 6 == 2), dtype=np.bool)
for i in range(1, int(n**0.5 / 3 + 1)):
if criba[i]:
k = 3 * i + 1 | 1
criba[k * k / 3::2 * k] = False
criba[k * (k - 2 * (i & 1) + 4) / 3::2 * k] = False
return np.r_[2, 3, ((3 * np.nonzero(criba)[0][1:] + 1) | 1)]
def goldbach(n):
"""imprime la composición de goldbach para n.
>>> goldbach(28)
(5, 23)
"""
primos = criba_primos(n)
lo = 0
hi = len(primos) - 1
while lo <= hi:
sum = primos[lo] + primos[hi]
if sum == n:
break
elif sum < n:
lo += 1
else:
hi -= 1
else:
print("No se encontro resultado de la conjetura de Goldbach para {}".format(n))
return primos[lo], primos[hi]
def goldbach_list(lower, upper):
"""Imprime la composición de Goldbach para todos los números pares
grandes que 'lower' y menores o iguales que 'upper'.
>>> goldbach_list(9,20)
10 = 3 + 7
12 = 5 + 7
14 = 3 + 11
16 = 3 + 13
18 = 5 + 13
20 = 3 + 17
"""
# La conjetura se aplica a pares mayores que 2.
if lower % 2 != 0:
lower += 1
if lower < 4:
lower = 4
if upper % 2 != 0:
upper -= 1
for n in range(lower, upper + 1, 2):
gb = goldbach(n)
print("{0} = {1} + {2}".format(n, gb[0], gb[1]))
# Goldbach entre 2000 y 2016
goldbach_list(2000, 2016)
# In[5]:
# Goldbach entre 9.999.980 y 10.000.000
goldbach_list(9999980, 10000000)
# In[6]:
# Goldbach entre 99.999.980 y 100.000.000
goldbach_list(99999980, 100000000)
# Con esto termino, el que quiera puede divertirse intentando comprobar la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)*, aunque corre el riesgo de terminar desperdiciando su tiempo como el bueno del tío Petros en la novela. Espero que les haya parecido interesante el artículo.
#
# Saludos!
#
# *Este post fue escrito utilizando IPython notebook. Pueden descargar este [notebook](https://github.com/relopezbriega/relopezbriega.github.io/blob/master/downloads/pygoldbach.ipynb) o ver su versión estática en [nbviewer](http://nbviewer.ipython.org/github/relopezbriega/relopezbriega.github.io/blob/master/downloads/pygoldbach.ipynb).*
#
# ### Ejemplo en Python
#
# Veamos un ejemplo en [Python](https://www.python.org/) de como implementar la [criba de Eratóstenes](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes) y un proceso de [factorización de primos](https://es.wikipedia.org/wiki/Factorizaci%C3%B3n_de_enteros).
# In[1]:
# Factorizando primos en Python
import numpy as np
def criba_eratostenes(n):
"""Criba Eratostenes"""
l=[]
multiplos = set()
for i in range(2, n+1):
if i not in multiplos:
l.append(i)
multiplos.update(range(i*i, n+1, i))
return l
def factorizar_primos(n):
"""Factoriza un entero positivo en primos
>>>factorizar_primos(28)
[2, 2, 7]
"""
if n <=1:
return "Ingresar un entero mayor a 1"
factores = []
primos = criba_eratostenes(n)
pindex = 0
p = primos[pindex]
num = n
while p != num:
if num % p == 0:
factores.append(p)
num //= p
else:
pindex += 1
p = primos[pindex]
factores.append(p)
return factores
factorizar_primos(28) # Factores primos de 28
# In[2]:
# Factores primos de 1982
factorizar_primos(1982)
# In[3]:
# Factores primos de 2015
factorizar_primos(2015)
# ## La conjetura de Goldbach y Python
#
# La *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)*, es otro ejemplo de como también podemos construir todos los números enteros con simples operaciones aritméticas como la suma y no más que tres *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*. Al día de hoy, la [conjetura](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach) continua sin poder ser demostrada; y es considerada uno de los problemas más difíciles de las matemáticas. La mayoría de los matemáticos estiman que es verdadera, ya que se ha mostrado cierta hasta por lo menos el $10^{18}$; aunque algunos dudan que sea cierta para números extremadamente grandes, el gran [Ramanujan](https://es.wikipedia.org/wiki/Srinivasa_Aiyangar_Ramanujan) dicen que se incluía en este último grupo.
#
# Obviamente, como este blog esta dedicado a [Python](https://www.python.org/), no podría concluir este artículo sin incluir una implementación de la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)* en uno de los lenguajes que mejor se lleva con las matemáticas!
#
# En esta implementación vamos a utilizar tres funciones, en primer lugar una [criba de primos](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes) vectorizada utilizando [numpy](http://www.numpy.org/), para lograr un mejor rendimiento que con la [criba de Eratóstenes](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes) del ejemplo anterior; y luego vamos a tener dos sencillas funciones adicionales, una que nos devuelva la composición de Goldbach para cualquier número par que le pasemos como parámetro.(esta función solo nos va a devolver la primer solución que encuentra, ya que pueden existir varias soluciones para algunos enteros pares). Por último, la restante función va a listar los resultados de la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)* para un rango de números enteros.
# In[4]:
# La conjetura de Goldbach en Python
import numpy as np
def criba_primos(n):
"""Criba generadora de números primos.
Input n>=6, devuleve un array de primos, 2 <= p < n
"""
criba = np.ones(n / 3 + (n % 6 == 2), dtype=np.bool)
for i in range(1, int(n**0.5 / 3 + 1)):
if criba[i]:
k = 3 * i + 1 | 1
criba[k * k / 3::2 * k] = False
criba[k * (k - 2 * (i & 1) + 4) / 3::2 * k] = False
return np.r_[2, 3, ((3 * np.nonzero(criba)[0][1:] + 1) | 1)]
def goldbach(n):
"""imprime la composición de goldbach para n.
>>> goldbach(28)
(5, 23)
"""
primos = criba_primos(n)
lo = 0
hi = len(primos) - 1
while lo <= hi:
sum = primos[lo] + primos[hi]
if sum == n:
break
elif sum < n:
lo += 1
else:
hi -= 1
else:
print("No se encontro resultado de la conjetura de Goldbach para {}".format(n))
return primos[lo], primos[hi]
def goldbach_list(lower, upper):
"""Imprime la composición de Goldbach para todos los números pares
grandes que 'lower' y menores o iguales que 'upper'.
>>> goldbach_list(9,20)
10 = 3 + 7
12 = 5 + 7
14 = 3 + 11
16 = 3 + 13
18 = 5 + 13
20 = 3 + 17
"""
# La conjetura se aplica a pares mayores que 2.
if lower % 2 != 0:
lower += 1
if lower < 4:
lower = 4
if upper % 2 != 0:
upper -= 1
for n in range(lower, upper + 1, 2):
gb = goldbach(n)
print("{0} = {1} + {2}".format(n, gb[0], gb[1]))
# Goldbach entre 2000 y 2016
goldbach_list(2000, 2016)
# In[5]:
# Goldbach entre 9.999.980 y 10.000.000
goldbach_list(9999980, 10000000)
# In[6]:
# Goldbach entre 99.999.980 y 100.000.000
goldbach_list(99999980, 100000000)
# Con esto termino, el que quiera puede divertirse intentando comprobar la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)*, aunque corre el riesgo de terminar desperdiciando su tiempo como el bueno del tío Petros en la novela. Espero que les haya parecido interesante el artículo.
#
# Saludos!
#
# *Este post fue escrito utilizando IPython notebook. Pueden descargar este [notebook](https://github.com/relopezbriega/relopezbriega.github.io/blob/master/downloads/pygoldbach.ipynb) o ver su versión estática en [nbviewer](http://nbviewer.ipython.org/github/relopezbriega/relopezbriega.github.io/blob/master/downloads/pygoldbach.ipynb).*
 # ## El tío Petros y la conjetura
#
# Hace un tiempo atrás, quede atrapado en la lectura de la apasionante novela de Apostolos Doxiadis, [El tío Petros y la conjetura de Goldbach](http://www.amazon.es/El-tio-petros-conjetura-goldbach/dp/8440694903). La novela trata basicamente de la relación entre un joven, en busca de su vocación, y su tío, quien en el pasado fue un prodigio de las matemáticas, pero que luego se recluyó de su familia y de la comunidad científica consumido por el intento solitario de demostrar uno de los problemas abiertos más difíciles de la [teoría de números](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_n%C3%BAmeros), la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)*. Lo que más me sorprendió del problema que consumió la vida del querido tío Petros, es lo simple que es su enunciado; la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)* nos dice que ***"Todo número par mayor que 2 puede escribirse como suma de dos números primos."***
#
# Este enunciado, junto con la otra conjetura postulada por [Goldbach](https://es.wikipedia.org/wiki/Christian_Goldbach), conocida como la *[Conjetura debil de Goldbach](https://es.wikipedia.org/wiki/Conjetura_d%C3%A9bil_de_Goldbach)*, que nos dice que ***"Todo número impar mayor que 5 puede expresarse como suma de tres números primos."***; trae a colación el concepto de los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* como bloques constructores de los enteros.
# ## Los números primos
#
# Pero, ¿cómo es esto de que los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* pueden ser considerados como bloques constructores de los números enteros?
#
# Un *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* es un entero positivo que solo puede ser dividido en dos [factores](https://es.wikipedia.org/wiki/Divisibilidad) distintos, 1 y si mismo. De esta definición se desprende que el número 1 no es un *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* ya que solo puede ser dividido en un solo [factor](https://es.wikipedia.org/wiki/Divisibilidad); en cambio, el número 2 si es *[primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*, el único *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* que es par.
#
# La idea de que los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* pueden ser considerados como bloques constructores de los números enteros surge del enunciado del [Teorema fundamental de la aritmética](https://es.wikipedia.org/wiki/Teorema_fundamental_de_la_aritm%C3%A9tica) que nos dice que ***"Todo entero positivo puede ser representado de forma única como un producto de factores primos"***; así por ejemplo el número $28$ puede ser representado como $2^2 * 7$; o el $60$ como $2^2 * 3 * 5$. Este teorema es un concepto fundamental en [criptografía](https://es.wikipedia.org/wiki/Criptograf%C3%ADa), los principales algoritmos de cifrado que se utilizan hoy en día residen en la [factorización de primos](https://es.wikipedia.org/wiki/Factorizaci%C3%B3n_de_enteros), ya que es un proceso que requiere de mucho esfuerzo para calcularse mientras más grande sea el número que queremos factorizar.
#
# Otro aspecto interesante de los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* es que parecen surgir en forma aleatoria, hay veces que pueden aparecer en pares como (11, 13), (29, 31) o (59, 61) pero otras veces puede haber un largo intervalo entre ellos. Aún no se ha encontrado una formula que pueda predecir cual va a ser el próximo *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*. Como parece ser bastante difícil encontrar un patrón en los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*, el esfuerzo de los matemáticos paso de intentar encontrar un patrón a intentar comprender la distribución de los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* dentro de todos los enteros; es decir, intentar responder la pregunta de ¿Cuál es la probabilidad de que un número sea primo si elijo un número al azar en el rango de 0 a N?. Uno de los primeros en dar una respuesta bastante aproximada a esta pregunta fue [Gauss](https://es.wikipedia.org/wiki/Carl_Friedrich_Gauss), quien con tan solo 15 años de edad propuso la formula $\pi(x)\approx\frac{x}{ln(x)}$ para responder a esa pregunta.
#
# La formula propuesta [Gauss](https://es.wikipedia.org/wiki/Carl_Friedrich_Gauss) implica que a medida que los números se hacen cada vez más grandes, los
# *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* son cada vez más escasos. Esto es lo que se conoce como [teorema de los números primos](https://es.wikipedia.org/wiki/Teorema_de_los_n%C3%BAmeros_primos).
# A pesar de que los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* son cada vez más escasos mientras más grandes, siguen surgiendo indefinidamente, son infinitos; esto esta bien demostrado por el ya famoso [teorema de Euclides](https://es.wikipedia.org/wiki/Teorema_de_Euclides); quien incluyo una de las más bellas demostraciones de las matemáticas en su obra [Elementos](https://es.wikipedia.org/wiki/Elementos_de_Euclides) en el 300 AC.
#
# ### Encontrando los números primos
#
# Para encontrar todos los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* menores que un número N, uno de los algoritmos más eficientes y más fáciles de utilizar es lo que se conoce como la [criba de Eratóstenes](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes), el procedimiento que se utiliza consiste en crear una tabla con todos los números naturales comprendidos entre 2 y N, y luego ir tachando los números que no son primos de la siguiente manera: Comenzando por el 2, se tachan todos sus múltiplos; comenzando de nuevo, cuando se encuentra un número entero que no ha sido tachado, ese número es declarado primo, y se procede a tachar todos sus múltiplos, así sucesivamente. La siguiente animación describe el procedimiento graficamente.
#
# ## El tío Petros y la conjetura
#
# Hace un tiempo atrás, quede atrapado en la lectura de la apasionante novela de Apostolos Doxiadis, [El tío Petros y la conjetura de Goldbach](http://www.amazon.es/El-tio-petros-conjetura-goldbach/dp/8440694903). La novela trata basicamente de la relación entre un joven, en busca de su vocación, y su tío, quien en el pasado fue un prodigio de las matemáticas, pero que luego se recluyó de su familia y de la comunidad científica consumido por el intento solitario de demostrar uno de los problemas abiertos más difíciles de la [teoría de números](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_n%C3%BAmeros), la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)*. Lo que más me sorprendió del problema que consumió la vida del querido tío Petros, es lo simple que es su enunciado; la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)* nos dice que ***"Todo número par mayor que 2 puede escribirse como suma de dos números primos."***
#
# Este enunciado, junto con la otra conjetura postulada por [Goldbach](https://es.wikipedia.org/wiki/Christian_Goldbach), conocida como la *[Conjetura debil de Goldbach](https://es.wikipedia.org/wiki/Conjetura_d%C3%A9bil_de_Goldbach)*, que nos dice que ***"Todo número impar mayor que 5 puede expresarse como suma de tres números primos."***; trae a colación el concepto de los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* como bloques constructores de los enteros.
# ## Los números primos
#
# Pero, ¿cómo es esto de que los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* pueden ser considerados como bloques constructores de los números enteros?
#
# Un *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* es un entero positivo que solo puede ser dividido en dos [factores](https://es.wikipedia.org/wiki/Divisibilidad) distintos, 1 y si mismo. De esta definición se desprende que el número 1 no es un *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* ya que solo puede ser dividido en un solo [factor](https://es.wikipedia.org/wiki/Divisibilidad); en cambio, el número 2 si es *[primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*, el único *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* que es par.
#
# La idea de que los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* pueden ser considerados como bloques constructores de los números enteros surge del enunciado del [Teorema fundamental de la aritmética](https://es.wikipedia.org/wiki/Teorema_fundamental_de_la_aritm%C3%A9tica) que nos dice que ***"Todo entero positivo puede ser representado de forma única como un producto de factores primos"***; así por ejemplo el número $28$ puede ser representado como $2^2 * 7$; o el $60$ como $2^2 * 3 * 5$. Este teorema es un concepto fundamental en [criptografía](https://es.wikipedia.org/wiki/Criptograf%C3%ADa), los principales algoritmos de cifrado que se utilizan hoy en día residen en la [factorización de primos](https://es.wikipedia.org/wiki/Factorizaci%C3%B3n_de_enteros), ya que es un proceso que requiere de mucho esfuerzo para calcularse mientras más grande sea el número que queremos factorizar.
#
# Otro aspecto interesante de los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* es que parecen surgir en forma aleatoria, hay veces que pueden aparecer en pares como (11, 13), (29, 31) o (59, 61) pero otras veces puede haber un largo intervalo entre ellos. Aún no se ha encontrado una formula que pueda predecir cual va a ser el próximo *[número primo](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*. Como parece ser bastante difícil encontrar un patrón en los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*, el esfuerzo de los matemáticos paso de intentar encontrar un patrón a intentar comprender la distribución de los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* dentro de todos los enteros; es decir, intentar responder la pregunta de ¿Cuál es la probabilidad de que un número sea primo si elijo un número al azar en el rango de 0 a N?. Uno de los primeros en dar una respuesta bastante aproximada a esta pregunta fue [Gauss](https://es.wikipedia.org/wiki/Carl_Friedrich_Gauss), quien con tan solo 15 años de edad propuso la formula $\pi(x)\approx\frac{x}{ln(x)}$ para responder a esa pregunta.
#
# La formula propuesta [Gauss](https://es.wikipedia.org/wiki/Carl_Friedrich_Gauss) implica que a medida que los números se hacen cada vez más grandes, los
# *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* son cada vez más escasos. Esto es lo que se conoce como [teorema de los números primos](https://es.wikipedia.org/wiki/Teorema_de_los_n%C3%BAmeros_primos).
# A pesar de que los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* son cada vez más escasos mientras más grandes, siguen surgiendo indefinidamente, son infinitos; esto esta bien demostrado por el ya famoso [teorema de Euclides](https://es.wikipedia.org/wiki/Teorema_de_Euclides); quien incluyo una de las más bellas demostraciones de las matemáticas en su obra [Elementos](https://es.wikipedia.org/wiki/Elementos_de_Euclides) en el 300 AC.
#
# ### Encontrando los números primos
#
# Para encontrar todos los *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)* menores que un número N, uno de los algoritmos más eficientes y más fáciles de utilizar es lo que se conoce como la [criba de Eratóstenes](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes), el procedimiento que se utiliza consiste en crear una tabla con todos los números naturales comprendidos entre 2 y N, y luego ir tachando los números que no son primos de la siguiente manera: Comenzando por el 2, se tachan todos sus múltiplos; comenzando de nuevo, cuando se encuentra un número entero que no ha sido tachado, ese número es declarado primo, y se procede a tachar todos sus múltiplos, así sucesivamente. La siguiente animación describe el procedimiento graficamente.
#  #
# ### Ejemplo en Python
#
# Veamos un ejemplo en [Python](https://www.python.org/) de como implementar la [criba de Eratóstenes](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes) y un proceso de [factorización de primos](https://es.wikipedia.org/wiki/Factorizaci%C3%B3n_de_enteros).
# In[1]:
# Factorizando primos en Python
import numpy as np
def criba_eratostenes(n):
"""Criba Eratostenes"""
l=[]
multiplos = set()
for i in range(2, n+1):
if i not in multiplos:
l.append(i)
multiplos.update(range(i*i, n+1, i))
return l
def factorizar_primos(n):
"""Factoriza un entero positivo en primos
>>>factorizar_primos(28)
[2, 2, 7]
"""
if n <=1:
return "Ingresar un entero mayor a 1"
factores = []
primos = criba_eratostenes(n)
pindex = 0
p = primos[pindex]
num = n
while p != num:
if num % p == 0:
factores.append(p)
num //= p
else:
pindex += 1
p = primos[pindex]
factores.append(p)
return factores
factorizar_primos(28) # Factores primos de 28
# In[2]:
# Factores primos de 1982
factorizar_primos(1982)
# In[3]:
# Factores primos de 2015
factorizar_primos(2015)
# ## La conjetura de Goldbach y Python
#
# La *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)*, es otro ejemplo de como también podemos construir todos los números enteros con simples operaciones aritméticas como la suma y no más que tres *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*. Al día de hoy, la [conjetura](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach) continua sin poder ser demostrada; y es considerada uno de los problemas más difíciles de las matemáticas. La mayoría de los matemáticos estiman que es verdadera, ya que se ha mostrado cierta hasta por lo menos el $10^{18}$; aunque algunos dudan que sea cierta para números extremadamente grandes, el gran [Ramanujan](https://es.wikipedia.org/wiki/Srinivasa_Aiyangar_Ramanujan) dicen que se incluía en este último grupo.
#
# Obviamente, como este blog esta dedicado a [Python](https://www.python.org/), no podría concluir este artículo sin incluir una implementación de la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)* en uno de los lenguajes que mejor se lleva con las matemáticas!
#
# En esta implementación vamos a utilizar tres funciones, en primer lugar una [criba de primos](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes) vectorizada utilizando [numpy](http://www.numpy.org/), para lograr un mejor rendimiento que con la [criba de Eratóstenes](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes) del ejemplo anterior; y luego vamos a tener dos sencillas funciones adicionales, una que nos devuelva la composición de Goldbach para cualquier número par que le pasemos como parámetro.(esta función solo nos va a devolver la primer solución que encuentra, ya que pueden existir varias soluciones para algunos enteros pares). Por último, la restante función va a listar los resultados de la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)* para un rango de números enteros.
# In[4]:
# La conjetura de Goldbach en Python
import numpy as np
def criba_primos(n):
"""Criba generadora de números primos.
Input n>=6, devuleve un array de primos, 2 <= p < n
"""
criba = np.ones(n / 3 + (n % 6 == 2), dtype=np.bool)
for i in range(1, int(n**0.5 / 3 + 1)):
if criba[i]:
k = 3 * i + 1 | 1
criba[k * k / 3::2 * k] = False
criba[k * (k - 2 * (i & 1) + 4) / 3::2 * k] = False
return np.r_[2, 3, ((3 * np.nonzero(criba)[0][1:] + 1) | 1)]
def goldbach(n):
"""imprime la composición de goldbach para n.
>>> goldbach(28)
(5, 23)
"""
primos = criba_primos(n)
lo = 0
hi = len(primos) - 1
while lo <= hi:
sum = primos[lo] + primos[hi]
if sum == n:
break
elif sum < n:
lo += 1
else:
hi -= 1
else:
print("No se encontro resultado de la conjetura de Goldbach para {}".format(n))
return primos[lo], primos[hi]
def goldbach_list(lower, upper):
"""Imprime la composición de Goldbach para todos los números pares
grandes que 'lower' y menores o iguales que 'upper'.
>>> goldbach_list(9,20)
10 = 3 + 7
12 = 5 + 7
14 = 3 + 11
16 = 3 + 13
18 = 5 + 13
20 = 3 + 17
"""
# La conjetura se aplica a pares mayores que 2.
if lower % 2 != 0:
lower += 1
if lower < 4:
lower = 4
if upper % 2 != 0:
upper -= 1
for n in range(lower, upper + 1, 2):
gb = goldbach(n)
print("{0} = {1} + {2}".format(n, gb[0], gb[1]))
# Goldbach entre 2000 y 2016
goldbach_list(2000, 2016)
# In[5]:
# Goldbach entre 9.999.980 y 10.000.000
goldbach_list(9999980, 10000000)
# In[6]:
# Goldbach entre 99.999.980 y 100.000.000
goldbach_list(99999980, 100000000)
# Con esto termino, el que quiera puede divertirse intentando comprobar la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)*, aunque corre el riesgo de terminar desperdiciando su tiempo como el bueno del tío Petros en la novela. Espero que les haya parecido interesante el artículo.
#
# Saludos!
#
# *Este post fue escrito utilizando IPython notebook. Pueden descargar este [notebook](https://github.com/relopezbriega/relopezbriega.github.io/blob/master/downloads/pygoldbach.ipynb) o ver su versión estática en [nbviewer](http://nbviewer.ipython.org/github/relopezbriega/relopezbriega.github.io/blob/master/downloads/pygoldbach.ipynb).*
#
# ### Ejemplo en Python
#
# Veamos un ejemplo en [Python](https://www.python.org/) de como implementar la [criba de Eratóstenes](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes) y un proceso de [factorización de primos](https://es.wikipedia.org/wiki/Factorizaci%C3%B3n_de_enteros).
# In[1]:
# Factorizando primos en Python
import numpy as np
def criba_eratostenes(n):
"""Criba Eratostenes"""
l=[]
multiplos = set()
for i in range(2, n+1):
if i not in multiplos:
l.append(i)
multiplos.update(range(i*i, n+1, i))
return l
def factorizar_primos(n):
"""Factoriza un entero positivo en primos
>>>factorizar_primos(28)
[2, 2, 7]
"""
if n <=1:
return "Ingresar un entero mayor a 1"
factores = []
primos = criba_eratostenes(n)
pindex = 0
p = primos[pindex]
num = n
while p != num:
if num % p == 0:
factores.append(p)
num //= p
else:
pindex += 1
p = primos[pindex]
factores.append(p)
return factores
factorizar_primos(28) # Factores primos de 28
# In[2]:
# Factores primos de 1982
factorizar_primos(1982)
# In[3]:
# Factores primos de 2015
factorizar_primos(2015)
# ## La conjetura de Goldbach y Python
#
# La *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)*, es otro ejemplo de como también podemos construir todos los números enteros con simples operaciones aritméticas como la suma y no más que tres *[números primos](https://es.wikipedia.org/wiki/N%C3%BAmero_primo)*. Al día de hoy, la [conjetura](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach) continua sin poder ser demostrada; y es considerada uno de los problemas más difíciles de las matemáticas. La mayoría de los matemáticos estiman que es verdadera, ya que se ha mostrado cierta hasta por lo menos el $10^{18}$; aunque algunos dudan que sea cierta para números extremadamente grandes, el gran [Ramanujan](https://es.wikipedia.org/wiki/Srinivasa_Aiyangar_Ramanujan) dicen que se incluía en este último grupo.
#
# Obviamente, como este blog esta dedicado a [Python](https://www.python.org/), no podría concluir este artículo sin incluir una implementación de la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)* en uno de los lenguajes que mejor se lleva con las matemáticas!
#
# En esta implementación vamos a utilizar tres funciones, en primer lugar una [criba de primos](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes) vectorizada utilizando [numpy](http://www.numpy.org/), para lograr un mejor rendimiento que con la [criba de Eratóstenes](https://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes) del ejemplo anterior; y luego vamos a tener dos sencillas funciones adicionales, una que nos devuelva la composición de Goldbach para cualquier número par que le pasemos como parámetro.(esta función solo nos va a devolver la primer solución que encuentra, ya que pueden existir varias soluciones para algunos enteros pares). Por último, la restante función va a listar los resultados de la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)* para un rango de números enteros.
# In[4]:
# La conjetura de Goldbach en Python
import numpy as np
def criba_primos(n):
"""Criba generadora de números primos.
Input n>=6, devuleve un array de primos, 2 <= p < n
"""
criba = np.ones(n / 3 + (n % 6 == 2), dtype=np.bool)
for i in range(1, int(n**0.5 / 3 + 1)):
if criba[i]:
k = 3 * i + 1 | 1
criba[k * k / 3::2 * k] = False
criba[k * (k - 2 * (i & 1) + 4) / 3::2 * k] = False
return np.r_[2, 3, ((3 * np.nonzero(criba)[0][1:] + 1) | 1)]
def goldbach(n):
"""imprime la composición de goldbach para n.
>>> goldbach(28)
(5, 23)
"""
primos = criba_primos(n)
lo = 0
hi = len(primos) - 1
while lo <= hi:
sum = primos[lo] + primos[hi]
if sum == n:
break
elif sum < n:
lo += 1
else:
hi -= 1
else:
print("No se encontro resultado de la conjetura de Goldbach para {}".format(n))
return primos[lo], primos[hi]
def goldbach_list(lower, upper):
"""Imprime la composición de Goldbach para todos los números pares
grandes que 'lower' y menores o iguales que 'upper'.
>>> goldbach_list(9,20)
10 = 3 + 7
12 = 5 + 7
14 = 3 + 11
16 = 3 + 13
18 = 5 + 13
20 = 3 + 17
"""
# La conjetura se aplica a pares mayores que 2.
if lower % 2 != 0:
lower += 1
if lower < 4:
lower = 4
if upper % 2 != 0:
upper -= 1
for n in range(lower, upper + 1, 2):
gb = goldbach(n)
print("{0} = {1} + {2}".format(n, gb[0], gb[1]))
# Goldbach entre 2000 y 2016
goldbach_list(2000, 2016)
# In[5]:
# Goldbach entre 9.999.980 y 10.000.000
goldbach_list(9999980, 10000000)
# In[6]:
# Goldbach entre 99.999.980 y 100.000.000
goldbach_list(99999980, 100000000)
# Con esto termino, el que quiera puede divertirse intentando comprobar la *[Conjetura de Goldbach](https://es.wikipedia.org/wiki/Conjetura_de_Goldbach)*, aunque corre el riesgo de terminar desperdiciando su tiempo como el bueno del tío Petros en la novela. Espero que les haya parecido interesante el artículo.
#
# Saludos!
#
# *Este post fue escrito utilizando IPython notebook. Pueden descargar este [notebook](https://github.com/relopezbriega/relopezbriega.github.io/blob/master/downloads/pygoldbach.ipynb) o ver su versión estática en [nbviewer](http://nbviewer.ipython.org/github/relopezbriega/relopezbriega.github.io/blob/master/downloads/pygoldbach.ipynb).*