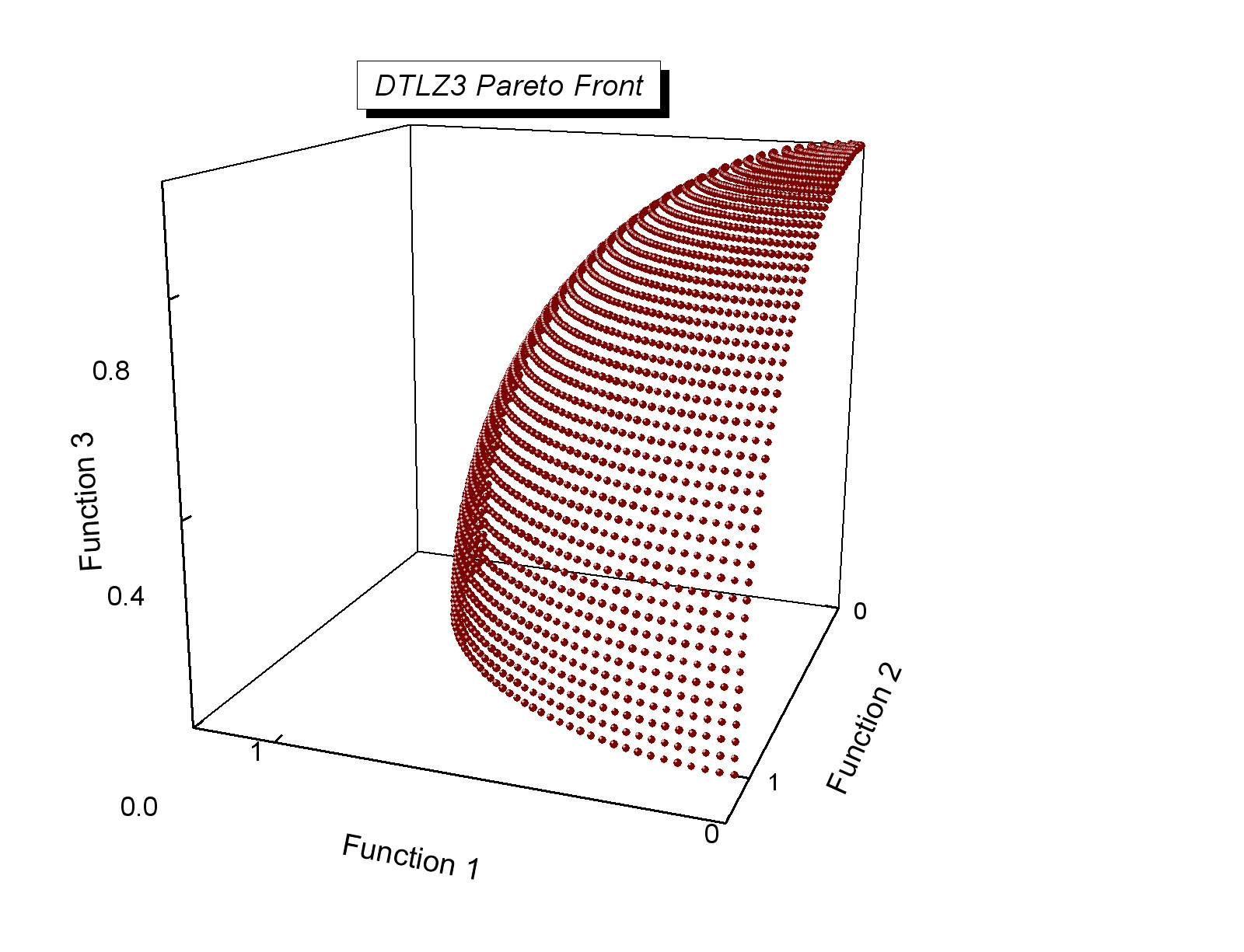
# from Coello Coello, Lamont and Van Veldhuizen (2007) Evolutionary Algorithms for Solving Multi-Objective Problems, Second Edition. Springer [Appendix E](http://www.cs.cinvestav.mx/~emoobook/apendix-e/apendix-e.html).
 #
#
#
#
#
#  #
#
#
#  # taken from http://xkcd.com/388/
# taken from http://xkcd.com/388/ # ## MOP (optimal) solutions
#
# Usually, there is not a unique solution that minimizes all objective functions simultaneously, but, instead, a set of equally good *trade-off* solutions.
#
# * *Optimality* can be defined in terms of the [*Pareto dominance*](https://en.wikipedia.org/wiki/Pareto_efficiency) relation. That is, having $\vec{x},\vec{y}\in\set{D}$, $\vec{x}$ is said to dominate $\vec{y}$ (expressed as $\vec{x}\dom\vec{y}$) iff $\forall f_j$, $f_j(\vec{x})\leq f_j(\vec{y})$ and $\exists f_i$ such that $f_i(\vec{x})< f_i(\vec{y})$.
# * Having the set $\set{A}$. $\set{A}^\ast$, the *non-dominated subset* of $\set{A}$, is defined as
#
# $$
# \set{A}^\ast=\left\{ \vec{x}\in\set{A} \left|\not\exists\vec{y}\in\set{A}:\vec{y}\dom\vec{x}\right.\right\}.
# $$
#
# * The *Pareto-optimal set*, $\set{D}^{\ast}$, is the solution of the problem. It is the subset of non-dominated elements of $\set{D}$. It is also known as the *efficient set*.
# * It consists of solutions that cannot be improved in any of the objectives without degrading at least one of the other objectives.
# * Its image in objective set is called the *Pareto-optimal front*, $\set{O}^\ast$.
# * Evolutionary algorithms generally yield a set of non-dominated solutions, $\set{P}^\ast$, that approximates $\set{D}^{\ast}$.
#
# As usual, we need some initialization and configuration.
# In[1]:
import time, array, random, copy, math
import numpy as np
import pandas as pd
# In[2]:
import matplotlib.pyplot as plt
get_ipython().run_line_magic('matplotlib', 'inline')
get_ipython().run_line_magic('config', "InlineBackend.figure_format = 'retina'")
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
plt.rcParams['text.latex.preamble'] ='\\usepackage{libertine}\n\\usepackage[utf8]{inputenc}'
import seaborn
seaborn.set(style='whitegrid')
seaborn.set_context('notebook')
# In[3]:
from deap import algorithms, base, benchmarks, tools, creator
# Planting a constant seed to always have the same results (and avoid surprises in class). -*you should not do this in a real-world case!*
# In[4]:
random.seed(a=42)
# # Visualizing the Pareto dominance relation
#
# * To start, lets have a visual example of the Pareto dominance relationship in action.
# * In this notebook we will deal with two-objective problems in order to simplify visualization.
# * Therefore, we can create:
# In[5]:
creator.create("FitnessMin", base.Fitness, weights=(-1.0,-1.0))
creator.create("Individual", array.array, typecode='d',
fitness=creator.FitnessMin)
# ## Let's use an illustrative MOP problem: Dent
#
# $$
# \begin{array}{rl}
# \text{minimize} & f_1(\vec{x}),f_2(\vec{x}) \\
# \text{such that} & f_1(\vec{x}) = \frac{1}{2}\left( \sqrt{1 + (x_1 + x_2)^2} \sqrt{1 + (x_1 - x_2)^2} + x_1 -x_2\right) + d,\\
# & f_2(\vec{x}) = \frac{1}{2}\left( \sqrt{1 + (x_1 + x_2)^2} \sqrt{1 + (x_1 - x_2)^2} - x_1 -x_2\right) + d,\\
# \text{with}& d = \lambda e^{-\left(x_1-x_2\right)^2}\ (\text{generally }\lambda=0.85) \text{ and } \vec{x}\in \left[-1.5,1.5\right]^2.
# \end{array}
# $$
# Implementing the Dent problem
# In[6]:
def dent(individual, lbda = 0.85):
"""
Implements the test problem Dent
Num. variables = 2; bounds in [-1.5, 1.5]; num. objetives = 2.
@author Cesar Revelo
"""
d = lbda * math.exp(-(individual[0] - individual[1]) ** 2)
f1 = 0.5 * (math.sqrt(1 + (individual[0] + individual[1]) ** 2) + \
math.sqrt(1 + (individual[0] - individual[1]) ** 2) + \
individual[0] - individual[1]) + d
f2 = 0.5 * (math.sqrt(1 + (individual[0] + individual[1]) ** 2) + \
math.sqrt(1 + (individual[0] - individual[1]) ** 2) - \
individual[0] + individual[1]) + d
return f1, f2
# Preparing a DEAP `toolbox` with Dent.
# In[7]:
toolbox = base.Toolbox()
# In[8]:
BOUND_LOW, BOUND_UP = -1.5, 1.5
NDIM = 2
# toolbox.register("evaluate", lambda ind: benchmarks.dtlz2(ind, 2))
toolbox.register("evaluate", dent)
# Defining attributes, individuals and population.
# In[9]:
def uniform(low, up, size=None):
try:
return [random.uniform(a, b) for a, b in zip(low, up)]
except TypeError:
return [random.uniform(a, b) for a, b in zip([low] * size, [up] * size)]
toolbox.register("attr_float", uniform, BOUND_LOW, BOUND_UP, NDIM)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.attr_float)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
# Creating an example population distributed as a mesh.
# In[10]:
num_samples = 50
limits = [np.arange(BOUND_LOW, BOUND_UP, (BOUND_UP - BOUND_LOW)/num_samples)] * NDIM
sample_x = np.meshgrid(*limits)
# In[11]:
flat = []
for i in range(len(sample_x)):
x_i = sample_x[i]
flat.append(x_i.reshape(num_samples**NDIM))
# In[12]:
example_pop = toolbox.population(n=num_samples**NDIM)
# In[13]:
for i, ind in enumerate(example_pop):
for j in range(len(flat)):
ind[j] = flat[j][i]
# In[14]:
fitnesses = toolbox.map(toolbox.evaluate, example_pop)
for ind, fit in zip(example_pop, fitnesses):
ind.fitness.values = fit
# We also need `a_given_individual`.
# In[15]:
a_given_individual = toolbox.population(n=1)[0]
a_given_individual[0] = 0.5
a_given_individual[1] = 0.5
# In[16]:
a_given_individual.fitness.values = toolbox.evaluate(a_given_individual)
# Implementing the Pareto dominance relation between two individulas.
# In[17]:
def pareto_dominance(ind1,ind2):
'Returns `True` if `ind1` dominates `ind2`.'
extrictly_better = False
for item1 in ind1.fitness.values:
for item2 in ind2.fitness.values:
if item1 > item2:
return False
if not extrictly_better and item1 < item2:
extrictly_better = True
return extrictly_better
# *Note:* Bear in mind that DEAP comes with a Pareto dominance relation that probably is more efficient than this implementation.
# ```python
# def pareto_dominance(x,y):
# return tools.emo.isDominated(x.fitness.values, y.fitness.values)
# ```
# Lets compute the set of individuals that are `dominated` by `a_given_individual`, the ones that dominate it (its `dominators`) and the remaining ones.
# In[18]:
dominated = [ind for ind in example_pop if pareto_dominance(a_given_individual, ind)]
dominators = [ind for ind in example_pop if pareto_dominance(ind, a_given_individual)]
others = [ind for ind in example_pop if not ind in dominated and not ind in dominators]
# In[19]:
def plot_dent():
'Plots the points in decision and objective spaces.'
plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
for ind in dominators: plt.plot(ind[0], ind[1], 'r.')
for ind in dominated: plt.plot(ind[0], ind[1], 'g.')
for ind in others: plt.plot(ind[0], ind[1], 'k.', ms=3)
plt.plot(a_given_individual[0], a_given_individual[1], 'bo', ms=6);
plt.xlabel('$x_1$');plt.ylabel('$x_2$');
plt.title('Decision space');
plt.subplot(1,2,2)
for ind in dominators: plt.plot(ind.fitness.values[0], ind.fitness.values[1], 'r.', alpha=0.7)
for ind in dominated: plt.plot(ind.fitness.values[0], ind.fitness.values[1], 'g.', alpha=0.7)
for ind in others: plt.plot(ind.fitness.values[0], ind.fitness.values[1], 'k.', alpha=0.7, ms=3)
plt.plot(a_given_individual.fitness.values[0], a_given_individual.fitness.values[1], 'bo', ms=6);
plt.xlabel('$f_1(\mathbf{x})$');plt.ylabel('$f_2(\mathbf{x})$');
plt.xlim((0.5,3.6));plt.ylim((0.5,3.6));
plt.title('Objective space');
plt.tight_layout()
# Having `a_given_individual` (blue dot) we can now plot those that are dominated by it (in green), those that dominate it (in red) and those that are uncomparable.
# In[20]:
plot_dent()
# Obtaining the nondominated front.
# In[21]:
non_dom = tools.sortNondominated(example_pop, k=len(example_pop), first_front_only=True)[0]
# In[22]:
plt.figure(figsize=(5,5))
for ind in example_pop:
plt.plot(ind.fitness.values[0], ind.fitness.values[1], 'k.', ms=3, alpha=0.5)
for ind in non_dom:
plt.plot(ind.fitness.values[0], ind.fitness.values[1], 'bo', alpha=0.74, ms=5)
plt.title('Pareto-optimal front')
# # The Non-dominated Sorting Genetic Algorithm (NSGA-II)
#
# * NSGA-II algorithm is one of the pillars of the EMO field.
# * Deb, K., Pratap, A., Agarwal, S., Meyarivan, T., *A fast and elitist multiobjective genetic algorithm: NSGA-II*, IEEE Transactions on Evolutionary Computation, vol.6, no.2, pp.182,197, Apr 2002 doi: [10.1109/4235.996017](http://dx.doi.org/10.1109/4235.996017).
# * Fitness assignment relies on the Pareto dominance relation:
# 1. Rank individuals according the dominance relations established between them.
# 2. Individuals with the same domination rank are then compared using a local crowding distance.
# ## NSGA-II fitness in detail
#
# * The first step consists in classifying the individuals in a series of categories $\mathcal{F}_1,\ldots,\mathcal{F}_L$.
# * Each of these categories store individuals that are only dominated by the elements of the previous categories,
# $$
# \begin{array}{rl}
# \forall \vec{x}\in\set{F}_i: &\exists \vec{y}\in\set{F}_{i-1} \text{ such that } \vec{y}\dom\vec{x},\text{ and }\\
# &\not\exists\vec{z}\in \set{P}_t\setminus\left( \set{F}_1\cup\ldots\cup\set{F}_{i-1}
# \right)\text{ that }\vec{z}\dom\vec{x}\,;
# \end{array}
# $$
# with $\mathcal{F}_1$ equal to $\mathcal{P}_t^\ast$, the set of non-dominated individuals of $\mathcal{P}_t$.
#
# * After all individuals are ranked a local crowding distance is assigned to them.
# * The use of this distance primes individuals more isolated with respect to others.
# ## Crowding distance
#
# The assignment process goes as follows,
#
# * for each category set $\set{F}_l$, having $f_l=|\set{F}_l|$,
# * for each individual $\vec{x}_i\in\set{F}_l$, set $d_{i}=0$.
# * for each objective function $m=1,\ldots,M$,
# * $\vec{I}=\mathrm{sort}\left(\set{F}_l,m\right)$ (generate index vector).
# * $d_{I_1}^{(l)}=d_{I_{f_l}}^{(l)}=\infty$.
# * for $i=2,\ldots,f_l-1$,
# * Update the remaining distances as,
# $$
# d_i = d_i + \frac{f_m\left(\vec{x}_{I_{i+1}}\right)-f_m\left(\vec{x}_{I_{i+1}}\right)}
# {f_m\left(\vec{x}_{I_{1}}\right)-f_m\left(\vec{x}_{I_{f_l}}\right)}\,.
# $$
#
# Here the $\mathrm{sort}\left(\set{F},m\right)$ function produces an ordered index vector $\vec{I}$ with respect to objective function $m$.
# Sorting the population by rank and distance.
#
# * Having the individual ranks and their local distances they are sorted using the crowded comparison operator, stated as:
# * An individual $\vec{x}_i$ _is better than_ $\vec{x}_j$ if:
# * $\vec{x}_i$ has a better rank: $\vec{x}_i\in\set{F}_k$, $\vec{x}_j\in\set{F}_l$ and $k
# ## MOP (optimal) solutions
#
# Usually, there is not a unique solution that minimizes all objective functions simultaneously, but, instead, a set of equally good *trade-off* solutions.
#
# * *Optimality* can be defined in terms of the [*Pareto dominance*](https://en.wikipedia.org/wiki/Pareto_efficiency) relation. That is, having $\vec{x},\vec{y}\in\set{D}$, $\vec{x}$ is said to dominate $\vec{y}$ (expressed as $\vec{x}\dom\vec{y}$) iff $\forall f_j$, $f_j(\vec{x})\leq f_j(\vec{y})$ and $\exists f_i$ such that $f_i(\vec{x})< f_i(\vec{y})$.
# * Having the set $\set{A}$. $\set{A}^\ast$, the *non-dominated subset* of $\set{A}$, is defined as
#
# $$
# \set{A}^\ast=\left\{ \vec{x}\in\set{A} \left|\not\exists\vec{y}\in\set{A}:\vec{y}\dom\vec{x}\right.\right\}.
# $$
#
# * The *Pareto-optimal set*, $\set{D}^{\ast}$, is the solution of the problem. It is the subset of non-dominated elements of $\set{D}$. It is also known as the *efficient set*.
# * It consists of solutions that cannot be improved in any of the objectives without degrading at least one of the other objectives.
# * Its image in objective set is called the *Pareto-optimal front*, $\set{O}^\ast$.
# * Evolutionary algorithms generally yield a set of non-dominated solutions, $\set{P}^\ast$, that approximates $\set{D}^{\ast}$.
#
# As usual, we need some initialization and configuration.
# In[1]:
import time, array, random, copy, math
import numpy as np
import pandas as pd
# In[2]:
import matplotlib.pyplot as plt
get_ipython().run_line_magic('matplotlib', 'inline')
get_ipython().run_line_magic('config', "InlineBackend.figure_format = 'retina'")
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
plt.rcParams['text.latex.preamble'] ='\\usepackage{libertine}\n\\usepackage[utf8]{inputenc}'
import seaborn
seaborn.set(style='whitegrid')
seaborn.set_context('notebook')
# In[3]:
from deap import algorithms, base, benchmarks, tools, creator
# Planting a constant seed to always have the same results (and avoid surprises in class). -*you should not do this in a real-world case!*
# In[4]:
random.seed(a=42)
# # Visualizing the Pareto dominance relation
#
# * To start, lets have a visual example of the Pareto dominance relationship in action.
# * In this notebook we will deal with two-objective problems in order to simplify visualization.
# * Therefore, we can create:
# In[5]:
creator.create("FitnessMin", base.Fitness, weights=(-1.0,-1.0))
creator.create("Individual", array.array, typecode='d',
fitness=creator.FitnessMin)
# ## Let's use an illustrative MOP problem: Dent
#
# $$
# \begin{array}{rl}
# \text{minimize} & f_1(\vec{x}),f_2(\vec{x}) \\
# \text{such that} & f_1(\vec{x}) = \frac{1}{2}\left( \sqrt{1 + (x_1 + x_2)^2} \sqrt{1 + (x_1 - x_2)^2} + x_1 -x_2\right) + d,\\
# & f_2(\vec{x}) = \frac{1}{2}\left( \sqrt{1 + (x_1 + x_2)^2} \sqrt{1 + (x_1 - x_2)^2} - x_1 -x_2\right) + d,\\
# \text{with}& d = \lambda e^{-\left(x_1-x_2\right)^2}\ (\text{generally }\lambda=0.85) \text{ and } \vec{x}\in \left[-1.5,1.5\right]^2.
# \end{array}
# $$
# Implementing the Dent problem
# In[6]:
def dent(individual, lbda = 0.85):
"""
Implements the test problem Dent
Num. variables = 2; bounds in [-1.5, 1.5]; num. objetives = 2.
@author Cesar Revelo
"""
d = lbda * math.exp(-(individual[0] - individual[1]) ** 2)
f1 = 0.5 * (math.sqrt(1 + (individual[0] + individual[1]) ** 2) + \
math.sqrt(1 + (individual[0] - individual[1]) ** 2) + \
individual[0] - individual[1]) + d
f2 = 0.5 * (math.sqrt(1 + (individual[0] + individual[1]) ** 2) + \
math.sqrt(1 + (individual[0] - individual[1]) ** 2) - \
individual[0] + individual[1]) + d
return f1, f2
# Preparing a DEAP `toolbox` with Dent.
# In[7]:
toolbox = base.Toolbox()
# In[8]:
BOUND_LOW, BOUND_UP = -1.5, 1.5
NDIM = 2
# toolbox.register("evaluate", lambda ind: benchmarks.dtlz2(ind, 2))
toolbox.register("evaluate", dent)
# Defining attributes, individuals and population.
# In[9]:
def uniform(low, up, size=None):
try:
return [random.uniform(a, b) for a, b in zip(low, up)]
except TypeError:
return [random.uniform(a, b) for a, b in zip([low] * size, [up] * size)]
toolbox.register("attr_float", uniform, BOUND_LOW, BOUND_UP, NDIM)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.attr_float)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
# Creating an example population distributed as a mesh.
# In[10]:
num_samples = 50
limits = [np.arange(BOUND_LOW, BOUND_UP, (BOUND_UP - BOUND_LOW)/num_samples)] * NDIM
sample_x = np.meshgrid(*limits)
# In[11]:
flat = []
for i in range(len(sample_x)):
x_i = sample_x[i]
flat.append(x_i.reshape(num_samples**NDIM))
# In[12]:
example_pop = toolbox.population(n=num_samples**NDIM)
# In[13]:
for i, ind in enumerate(example_pop):
for j in range(len(flat)):
ind[j] = flat[j][i]
# In[14]:
fitnesses = toolbox.map(toolbox.evaluate, example_pop)
for ind, fit in zip(example_pop, fitnesses):
ind.fitness.values = fit
# We also need `a_given_individual`.
# In[15]:
a_given_individual = toolbox.population(n=1)[0]
a_given_individual[0] = 0.5
a_given_individual[1] = 0.5
# In[16]:
a_given_individual.fitness.values = toolbox.evaluate(a_given_individual)
# Implementing the Pareto dominance relation between two individulas.
# In[17]:
def pareto_dominance(ind1,ind2):
'Returns `True` if `ind1` dominates `ind2`.'
extrictly_better = False
for item1 in ind1.fitness.values:
for item2 in ind2.fitness.values:
if item1 > item2:
return False
if not extrictly_better and item1 < item2:
extrictly_better = True
return extrictly_better
# *Note:* Bear in mind that DEAP comes with a Pareto dominance relation that probably is more efficient than this implementation.
# ```python
# def pareto_dominance(x,y):
# return tools.emo.isDominated(x.fitness.values, y.fitness.values)
# ```
# Lets compute the set of individuals that are `dominated` by `a_given_individual`, the ones that dominate it (its `dominators`) and the remaining ones.
# In[18]:
dominated = [ind for ind in example_pop if pareto_dominance(a_given_individual, ind)]
dominators = [ind for ind in example_pop if pareto_dominance(ind, a_given_individual)]
others = [ind for ind in example_pop if not ind in dominated and not ind in dominators]
# In[19]:
def plot_dent():
'Plots the points in decision and objective spaces.'
plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
for ind in dominators: plt.plot(ind[0], ind[1], 'r.')
for ind in dominated: plt.plot(ind[0], ind[1], 'g.')
for ind in others: plt.plot(ind[0], ind[1], 'k.', ms=3)
plt.plot(a_given_individual[0], a_given_individual[1], 'bo', ms=6);
plt.xlabel('$x_1$');plt.ylabel('$x_2$');
plt.title('Decision space');
plt.subplot(1,2,2)
for ind in dominators: plt.plot(ind.fitness.values[0], ind.fitness.values[1], 'r.', alpha=0.7)
for ind in dominated: plt.plot(ind.fitness.values[0], ind.fitness.values[1], 'g.', alpha=0.7)
for ind in others: plt.plot(ind.fitness.values[0], ind.fitness.values[1], 'k.', alpha=0.7, ms=3)
plt.plot(a_given_individual.fitness.values[0], a_given_individual.fitness.values[1], 'bo', ms=6);
plt.xlabel('$f_1(\mathbf{x})$');plt.ylabel('$f_2(\mathbf{x})$');
plt.xlim((0.5,3.6));plt.ylim((0.5,3.6));
plt.title('Objective space');
plt.tight_layout()
# Having `a_given_individual` (blue dot) we can now plot those that are dominated by it (in green), those that dominate it (in red) and those that are uncomparable.
# In[20]:
plot_dent()
# Obtaining the nondominated front.
# In[21]:
non_dom = tools.sortNondominated(example_pop, k=len(example_pop), first_front_only=True)[0]
# In[22]:
plt.figure(figsize=(5,5))
for ind in example_pop:
plt.plot(ind.fitness.values[0], ind.fitness.values[1], 'k.', ms=3, alpha=0.5)
for ind in non_dom:
plt.plot(ind.fitness.values[0], ind.fitness.values[1], 'bo', alpha=0.74, ms=5)
plt.title('Pareto-optimal front')
# # The Non-dominated Sorting Genetic Algorithm (NSGA-II)
#
# * NSGA-II algorithm is one of the pillars of the EMO field.
# * Deb, K., Pratap, A., Agarwal, S., Meyarivan, T., *A fast and elitist multiobjective genetic algorithm: NSGA-II*, IEEE Transactions on Evolutionary Computation, vol.6, no.2, pp.182,197, Apr 2002 doi: [10.1109/4235.996017](http://dx.doi.org/10.1109/4235.996017).
# * Fitness assignment relies on the Pareto dominance relation:
# 1. Rank individuals according the dominance relations established between them.
# 2. Individuals with the same domination rank are then compared using a local crowding distance.
# ## NSGA-II fitness in detail
#
# * The first step consists in classifying the individuals in a series of categories $\mathcal{F}_1,\ldots,\mathcal{F}_L$.
# * Each of these categories store individuals that are only dominated by the elements of the previous categories,
# $$
# \begin{array}{rl}
# \forall \vec{x}\in\set{F}_i: &\exists \vec{y}\in\set{F}_{i-1} \text{ such that } \vec{y}\dom\vec{x},\text{ and }\\
# &\not\exists\vec{z}\in \set{P}_t\setminus\left( \set{F}_1\cup\ldots\cup\set{F}_{i-1}
# \right)\text{ that }\vec{z}\dom\vec{x}\,;
# \end{array}
# $$
# with $\mathcal{F}_1$ equal to $\mathcal{P}_t^\ast$, the set of non-dominated individuals of $\mathcal{P}_t$.
#
# * After all individuals are ranked a local crowding distance is assigned to them.
# * The use of this distance primes individuals more isolated with respect to others.
# ## Crowding distance
#
# The assignment process goes as follows,
#
# * for each category set $\set{F}_l$, having $f_l=|\set{F}_l|$,
# * for each individual $\vec{x}_i\in\set{F}_l$, set $d_{i}=0$.
# * for each objective function $m=1,\ldots,M$,
# * $\vec{I}=\mathrm{sort}\left(\set{F}_l,m\right)$ (generate index vector).
# * $d_{I_1}^{(l)}=d_{I_{f_l}}^{(l)}=\infty$.
# * for $i=2,\ldots,f_l-1$,
# * Update the remaining distances as,
# $$
# d_i = d_i + \frac{f_m\left(\vec{x}_{I_{i+1}}\right)-f_m\left(\vec{x}_{I_{i+1}}\right)}
# {f_m\left(\vec{x}_{I_{1}}\right)-f_m\left(\vec{x}_{I_{f_l}}\right)}\,.
# $$
#
# Here the $\mathrm{sort}\left(\set{F},m\right)$ function produces an ordered index vector $\vec{I}$ with respect to objective function $m$.
# Sorting the population by rank and distance.
#
# * Having the individual ranks and their local distances they are sorted using the crowded comparison operator, stated as:
# * An individual $\vec{x}_i$ _is better than_ $\vec{x}_j$ if:
# * $\vec{x}_i$ has a better rank: $\vec{x}_i\in\set{F}_k$, $\vec{x}_j\in\set{F}_l$ and $k # from Coello Coello, Lamont and Van Veldhuizen (2007) Evolutionary Algorithms for Solving Multi-Objective Problems, Second Edition. Springer [Appendix E](http://www.cs.cinvestav.mx/~emoobook/apendix-e/apendix-e.html).
# from Coello Coello, Lamont and Van Veldhuizen (2007) Evolutionary Algorithms for Solving Multi-Objective Problems, Second Edition. Springer [Appendix E](http://www.cs.cinvestav.mx/~emoobook/apendix-e/apendix-e.html). #
#